
9.定义函数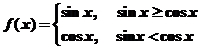 ,给出下列四个命题:(1)该函数的值域为
,给出下列四个命题:(1)该函数的值域为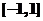 ;
;
(2)当且仅当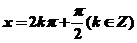 时,该函数取得最大值;(3)该函数是以
时,该函数取得最大值;(3)该函数是以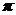 为最小正周期的周期函数;(4)当且仅当
为最小正周期的周期函数;(4)当且仅当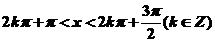 时,
时,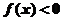 .上述命题中正确的个数是 (
.上述命题中正确的个数是 ( 
 )
)
A.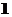 个 B.
个 B.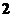 个
C.
个
C.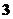 个 D.
个 D.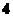 个
个
8.下列以行列式表达的结果中,与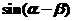 相等的是
( )
相等的是
( )
A.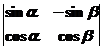
 B.
B.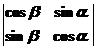 C.
C.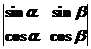 D.
D.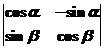
7.对任意的实数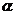 、
、 ,下列等式恒成立的
,下列等式恒成立的 是
( )
是
( )
A. 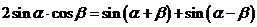 ;
;
B. 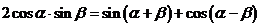 ;
;
C. 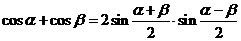 ;
;
D. 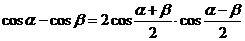 .
.
6.若角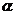 和角
和角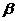 的终边关于
的终边关于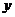 轴对称,则下列等式恒成立的是
( )
轴对称,则下列等式恒成立的是
( )
A. 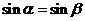 ; B.
; B. 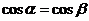 ; C.
; C. 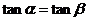 ; D.
; D. 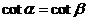 .
.
5.若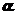 为第二象限角,则
为第二象限角,则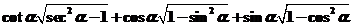 = ( )
= ( )
A.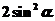 B.
B.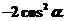 C.
C.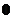 D.
D.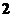 [来源:学.科.网Z.X.X.K]
[来源:学.科.网Z.X.X.K]
4.函数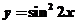 是一个( )
是一个( )
A.周期为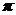 的奇函数 B.周期为
的奇函数 B.周期为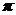 的偶函数
的偶函数
C.周期为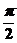 的奇函数 D.周期为
的奇函数 D.周期为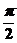 的偶函数
的偶函数
3.对于任意实数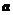 ,要使函数
,要使函数 在区间
在区间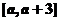 上的值
上的值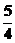 出现的次数不小于
出现的次数不小于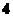 次,又不多于
次,又不多于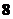 次,则
次,则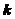 可以取
( )
可以取
( )
A. 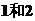 B.
B. 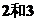 C.
C. 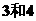 D.
D. 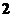
2.把函数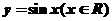 的图像上所有的点向左平行移动
的图像上所有的点向左平行移动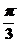 个单位长度,再把图像上所有点的横坐标缩短到原来的
个单位长度,再把图像上所有点的横坐标缩短到原来的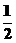 倍(纵坐标不变),得到的图
倍(纵坐标不变),得到的图 像所表示的函数是 ( )
像所表示的函数是 ( )
A. 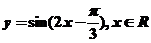 B.
B. 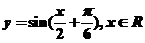
C. 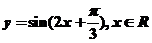 D.
D. 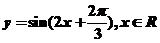
1.下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是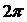 ;
;
②终边在y轴上的角的集合是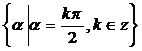 ;
;
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点;
④把函数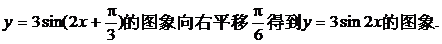 ;
;
⑤在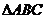 中,若
中,若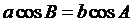 ,则
,则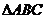 是等腰三角形
是等腰三角形 ;
;
其中真命题的序号是-------------------------------------( )
A.(1)(2)(3) B.(2)(3)(4) C.(3)(4)(5) D.(1)(4)(5)
15、①④析:①奇函数右移一个单位,对称中心成了(1,0);②式是周期性,不是对称性;③式是关于x=0对称;④f(x+1)=f(1-x)=f[(-2-x)+3]=f[3-(-2-x)]=f(5+x)
16解:①令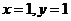 代入
代入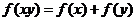 中得
中得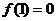 。(4分)
。(4分)
②令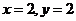 代入
代入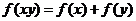 中得
中得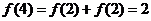 (6分)
(6分)
不等式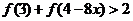 化为
化为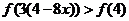 ;
;
又函数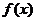 是定义在
是定义在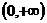 上的增函数,所以
上的增函数,所以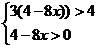
得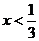 (12分)
(12分)
17解:①由题意得f'x(3,4)=6
f'y(3,4)=8(6分)
②由几何意义可求得z的最小值为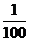 (12分)
(12分)
18解:①由题意,贷款额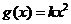 ,利息
,利息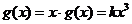 。(4分)
。(4分)
②李佳节省的钱(设为y)即为两种付款方式之间的利息差,则: 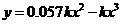 ,所以
,所以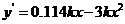
令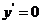 解得
解得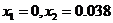 ,从而
,从而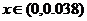 时,
时,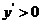 ;
;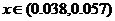 时,
时,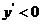 。
。
所以,当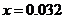 时,函数
时,函数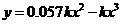 取到最大值,即
取到最大值,即
银行贷款利率为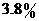 时,李佳可以节省最多的钱。(12分)
时,李佳可以节省最多的钱。(12分)
19解:由于f(x)=(x-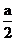 )
)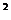 +
+ 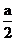 -
-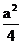
于是若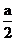 ∈[0
,1 ] ,即0
≤a ≤2
,则最小值为
∈[0
,1 ] ,即0
≤a ≤2
,则最小值为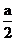 -
-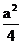
(3分)
若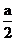 不属于[0
,1 ]则最小值为f(0)和f(1)中的最小者。(6分)
不属于[0
,1 ]则最小值为f(0)和f(1)中的最小者。(6分)
所以F(a):
当0 ≤a ≤2时为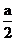 -
-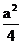
当a>2时为1-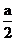
以下由二次函数知识可以求得当a =
1 时, F( a)
达到最大值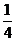 (12分)
(12分)
20解:对任意的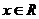 ,不等式
,不等式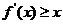 恒成立,即
恒成立,即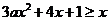 ,则
,则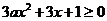 恒成立。(3分)
恒成立。(3分)
当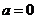 时,
时,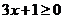 对任意的x不恒成立。(6分)
对任意的x不恒成立。(6分)
当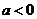 时,对任意的x不等式
时,对任意的x不等式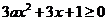 不能恒成立。
不能恒成立。
(9分)
当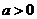 时,对任意的x不等式
时,对任意的x不等式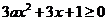 恒成立,则
恒成立,则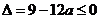 ,即
,即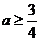 (12分)
(12分)
综上所述,实数a的取值范围是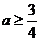 (13分)
(13分)
21解:①由题意得: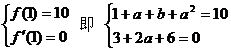
(2分,文科4)
解之得: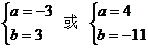 (4分,文科8分)
(4分,文科8分)
于是f(x)=x3+4x2-11x+16或f(x)=x3-3x2+3x+9
检验,当f(x)=x3-3x2+3x +9时,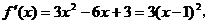 此时,尽管满足了
此时,尽管满足了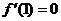 ,但在1的左右两侧的导数符号为同号,亦即x=1不是f(x)=x3-3x2+3x+9的极值点。
,但在1的左右两侧的导数符号为同号,亦即x=1不是f(x)=x3-3x2+3x+9的极值点。
∴f(x)=x3+4x2-11x+16(6分,文科10分)
②易求得其极值点为x=1和x=-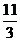 ,因而对称中心横坐标-
,因而对称中心横坐标-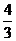 (8分,文科14分)
(8分,文科14分)
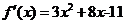 ,设直线PnPn-1是过点Pn且与f(x)的图像切于点Pn-1的切线,则一方面切线的斜率为
,设直线PnPn-1是过点Pn且与f(x)的图像切于点Pn-1的切线,则一方面切线的斜率为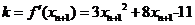 ,另一方面切线的斜率为:
,另一方面切线的斜率为: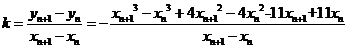
=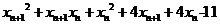
所以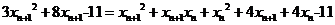 即
即
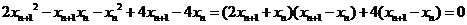 又因为
又因为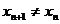 ,所以
,所以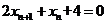 ,即
,即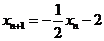 。
。
利用待定系数法易知: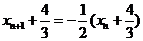 ,故数列
,故数列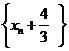 为等比数列,所以
为等比数列,所以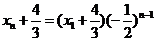 ,即
,即
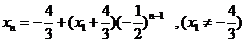 ,
,
则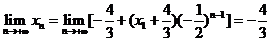 ,不难看出当n
,不难看出当n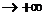 时,点列P1、P2、P3……Pn横坐标趋近于对称中心横坐标-
时,点列P1、P2、P3……Pn横坐标趋近于对称中心横坐标-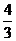 (14分)
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com