
5. [巩固1] D,[巩固2]B,
4. [巩固1] C, [巩固2] 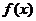 =2 cos(2x-
=2 cos(2x-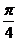 )
)
1. [巩固] ①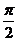 ②
②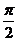 ③4
③4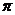 ;2.[巩固]①②④, [迁移] f(x)=2sin(2
;2.[巩固]①②④, [迁移] f(x)=2sin(2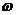 x-
x-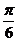 ), ①由f(x1)≤f(x)≤f(x2)知:x1、x2分别是函数y=f(x)的最小值、最大值点,最小、最大值点间最近的距离为半个周期,得
), ①由f(x1)≤f(x)≤f(x2)知:x1、x2分别是函数y=f(x)的最小值、最大值点,最小、最大值点间最近的距离为半个周期,得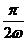 ,②偶,③视2
,②偶,③视2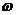 x-
x-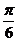 为一个角
为一个角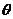 ,则
,则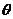 ∈[-
∈[-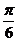 ,
,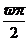 -
-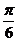 ],函数
],函数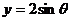 在 [-
在 [-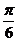 ,
,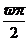 -
-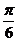 ]上单调,则
]上单调,则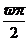 -
-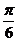 ≤
≤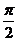 ,得0<
,得0<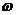 ≤
≤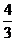 ,又
,又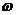 为整数,∴
为整数,∴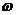 =1。3.[巩固] 注意A未必是正数,C, [迁移] y=3sin(
=1。3.[巩固] 注意A未必是正数,C, [迁移] y=3sin(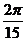 x+
x+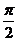 )+2
)+2
5.三角形三内角A、B、C成等差数列,当且仅当B=600;在△ABC中:A>B 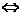 sinA>sinB;sin(B+C)=sinA、cos(B+C)=-cosA、cos
sinA>sinB;sin(B+C)=sinA、cos(B+C)=-cosA、cos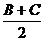 =sin
=sin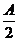 、sin
、sin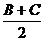 =cos
=cos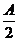 ;△ABC中cosA+cosB>0,cosB+cosC>0,cosA+cosC>0;在锐角三角形△ABC中sinA>cosB,sinB>cosC,
;△ABC中cosA+cosB>0,cosB+cosC>0,cosA+cosC>0;在锐角三角形△ABC中sinA>cosB,sinB>cosC,
sinC>cosA等;若A、B是钝角三角形两锐角,则sinA<cosB,sinB<cosA。等等
[举例] 在△ABC中,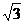 cos(B+C)+cos(
cos(B+C)+cos(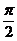 +A)的取值范围是
.
+A)的取值范围是
.
解析:原式=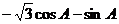 =-2sin(A+
=-2sin(A+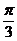 ),∵A∈(0,
),∵A∈(0,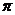 )
)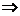 A+
A+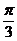 ∈(
∈(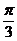 ,
,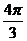 )
)
sin(A+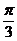 )∈(-
)∈(-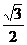 ,1
,1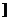 ,即原式的取值范围是:
,即原式的取值范围是: 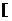 -2,
-2,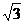 )
)
[巩固1]在锐角三角形△ABC中,设x=sinAsinB,y=cosAcosB,则x,y的大小关系是:( )
A.x≤y, B.x<y C.x≥y D.x>y
[巩固2] 在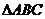 中,已知
中,已知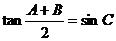 ,给出以下四个论断:①
,给出以下四个论断:①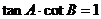 ,②
,②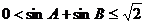 ,③
,③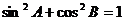 ,④
,④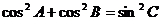 ,
,
其中正确的是( )
A.①③ B.②④ C.①④ D.②③
简答
4. 三角函数图象的平移变换、伸缩变换遵循“图进标退”原理:即图象向上(右)平移m(m>0)个单位,则表达式中的y(x)应变为y-m(x-m);图象横(纵)坐标变为原来的n倍,则表达式中的x(y)应变为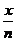 (
(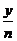 )。关注“先伸缩后平移”与“先平移后伸缩”的结果是不同的。
)。关注“先伸缩后平移”与“先平移后伸缩”的结果是不同的。
[举例] 已知函数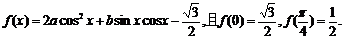
(Ⅰ)函数f(x)的图象经过怎样的平移才能使其对应的函数成为奇函数?
(Ⅱ)函数f(x)的图象经过怎样的平移后得到y=cosx.。
解析:由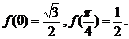 得:
得: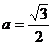 ,b=1,降次、“合二为一”后得:
,b=1,降次、“合二为一”后得: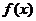 =sin(2x+
=sin(2x+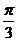 ),
),
(Ⅰ)思路一:函数y= f(x)的图象关于(-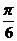 ,0)对称,向右平移
,0)对称,向右平移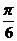 个单位后图象关于原点对称即为奇函数(平移的方法不唯一,因为函数y= f(x)的图象对称中心不唯一);
个单位后图象关于原点对称即为奇函数(平移的方法不唯一,因为函数y= f(x)的图象对称中心不唯一);
思路二:若函数f(x)的图象向右平移m个单位得到函数y= sin(2x-2m+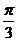 ),要使其为奇函数,则x=0时函数值为0(奇函数图象关于原点对称),即-2m+
),要使其为奇函数,则x=0时函数值为0(奇函数图象关于原点对称),即-2m+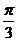 =
=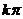 ,
,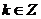
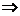 m=
m=
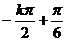 ,
,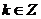 ,随
,随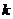 的取值不同可以得到不同的m的值,回答其中任一个即可。(运算量虽大一些,但更具一般性)。
的取值不同可以得到不同的m的值,回答其中任一个即可。(运算量虽大一些,但更具一般性)。
(Ⅱ) 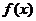 =sin(2x+
=sin(2x+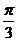 )=cos(
)=cos(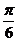 -2x)=cos(2x-
-2x)=cos(2x-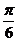 )=cos[2(x-
)=cos[2(x-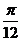 )],方案一:先左移
)],方案一:先左移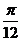 (x变成x+
(x变成x+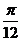 )得到函数y= cos2x,再纵坐标不变横坐标变为原来的2倍(x变成
)得到函数y= cos2x,再纵坐标不变横坐标变为原来的2倍(x变成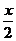 )得到函数y=cosx;
)得到函数y=cosx;
方案二:先纵坐标不变横坐标变为原来的2倍(x变成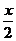 )得到函数y= cos(x-
)得到函数y= cos(x-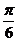 ),再左移
),再左移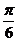 (x变成x+
(x变成x+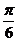 )得到函数y=cosx。注:(ⅰ)图象变换的问题要特别注意题目要求由谁变到谁,不要搞错了方向;(ⅱ)变换的源头和结果需化为同名的三角函数且角变量的系数同号(用诱导公式)才能实施;(ⅲ)如果已知变换的结果探究变换的源头,可以“倒行逆施”。
)得到函数y=cosx。注:(ⅰ)图象变换的问题要特别注意题目要求由谁变到谁,不要搞错了方向;(ⅱ)变换的源头和结果需化为同名的三角函数且角变量的系数同号(用诱导公式)才能实施;(ⅲ)如果已知变换的结果探究变换的源头,可以“倒行逆施”。
[巩固1]把函数y=cosx-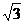 sinx的图象向左平移m个单位(m>0)所得的图象关于y轴对称,则m 的最小值是
sinx的图象向左平移m个单位(m>0)所得的图象关于y轴对称,则m 的最小值是
A.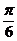 B.
B.
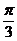 C.
C.
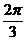 D.
D. 
[巩固2] 将函数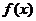 =Acos(ωx+φ)(A>0,ω>0, |φ|<
=Acos(ωx+φ)(A>0,ω>0, |φ|<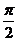 )的图象向右平移
)的图象向右平移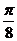 ,再横坐标伸长为原来的2倍、纵坐标缩小为原来的一半得到函数y=sinx,则
,再横坐标伸长为原来的2倍、纵坐标缩小为原来的一半得到函数y=sinx,则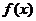 =
。
=
。
3.已知函数y=Asin(ωx+φ)+B(A>0,ω>0)的图象求表达式,一般先根据函数的最大值M、最小值m(最高、最低点的纵坐标),确定A、B(A+B=M,-A+B= m);根据相邻的最大、最小值点间的距离d(最高、最低点的横坐标之差的绝对值)确定ω(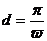 ),最后用最高(或最低)点的坐标代入表达式确定φ。
),最后用最高(或最低)点的坐标代入表达式确定φ。
[举例] 已知函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的两个相邻最值点为(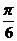 ,2), (
,2), (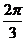 ,
,
-2),则这个函数的解析式为y =____________.
解析:A=2,相邻最值点相距半个周期,即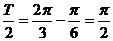 ,∴T=π
,∴T=π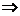 ω=2,
ω=2,
则函数解析式为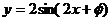 ,点(
,点(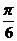 ,2)在函数图象上,∴2=2sin(
,2)在函数图象上,∴2=2sin(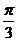 +φ)
+φ) 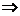
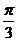 +φ=2
+φ=2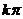 +
+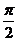 得φ=2
得φ=2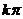 +
+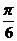 ,
,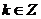 ∴函数的解析式为
∴函数的解析式为 。
。
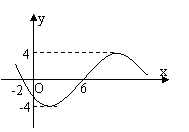 [巩固] 函数y=Asin(ωx+φ)(ω>0,|φ|<
[巩固] 函数y=Asin(ωx+φ)(ω>0,|φ|<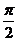 )的部分图象如右,
)的部分图象如右,
则函数表达式为:
A.y=-4sin(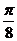 x+
x+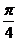 ),B.y=4sin(
),B.y=4sin(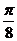 x-
x-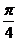 ),
),
 C.y=-4sin(
C.y=-4sin(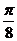 x-
x-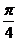 ),D.y=4sin(
),D.y=4sin(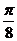 x+
x+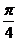 )
)
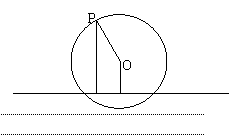
[迁移]如图是一个半径为3米的水轮,水轮圆心O距离水面
2米 ,已知水轮每分钟转动四圈,水轮上的点P相对于水面
,已知水轮每分钟转动四圈,水轮上的点P相对于水面
的高度y(米)与时间x(秒)满足函数关系y=Asin(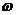 x+
x+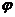 )+B
)+B
(A>0,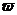 >0,0<
>0,0<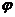 <2
<2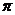 ),若x=0时,P在最高点,则函数
),若x=0时,P在最高点,则函数
表达式为:
2.在解决函数y=Asin(ωx+φ)的相关问题时,一般对ωx+φ作“整体化”处理。如:用“五点法”作函数y=Asin(ωx+φ)的图象时,应取ωx+φ=0、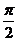 、
、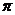 、
、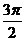 、2
、2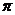 等,而不是取x等于它们;求函数y=Asin(ωx+φ)的取值范围时,应由x的范围确定ωx+φ的范围,再观察三角函数的图象(或单位圆上的三角函数线),注意:只需作出y=sin
等,而不是取x等于它们;求函数y=Asin(ωx+φ)的取值范围时,应由x的范围确定ωx+φ的范围,再观察三角函数的图象(或单位圆上的三角函数线),注意:只需作出y=sin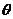 (把ωx+φ视为一个整体,即
(把ωx+φ视为一个整体,即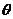 )的草图,而无需画y=Asin(ωx+φ)的图象;求函数y=Asin(ωx+φ)(ω>0)的单调区间时,也是视ωx+φ为一个整体,先指出ωx+φ的范围,再求x的范围;研究函数y=Asin(ωx+φ)的图象对称性时,则分别令ωx+φ=k
)的草图,而无需画y=Asin(ωx+φ)的图象;求函数y=Asin(ωx+φ)(ω>0)的单调区间时,也是视ωx+φ为一个整体,先指出ωx+φ的范围,再求x的范围;研究函数y=Asin(ωx+φ)的图象对称性时,则分别令ωx+φ=k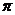 +
+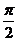 和ωx+φ=k
和ωx+φ=k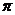 (k∈Z),从而得到函数y=Asin(ωx+φ)的图象关于直线
(k∈Z),从而得到函数y=Asin(ωx+φ)的图象关于直线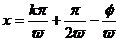 对称,关于点(
对称,关于点(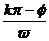 ,0)对称(k∈Z),(正、余弦函数图象的对称轴平行于Y轴且过函数图象的最高点或最低点,而对称中心是图象与“平衡轴”的交点);对函数y=Acos(ωx+φ)也作完全类似的处理。
,0)对称(k∈Z),(正、余弦函数图象的对称轴平行于Y轴且过函数图象的最高点或最低点,而对称中心是图象与“平衡轴”的交点);对函数y=Acos(ωx+φ)也作完全类似的处理。
[举例1]画出函数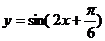 在[0,
在[0,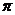 ]内的图象并指出其有无对称轴、对称中心。
]内的图象并指出其有无对称轴、对称中心。
解析:作函数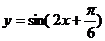 的图象不是先作函数
的图象不是先作函数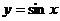 的图象,再由它伸宿、平移得到,而是直接描点作图。但不是在[0,
的图象,再由它伸宿、平移得到,而是直接描点作图。但不是在[0,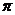 ]内取
]内取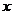 =0、
=0、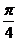 、
、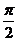 、
、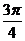 、
、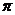 这五点,而是视
这五点,而是视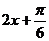 为一个角,
为一个角,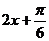 ∈[
∈[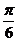 ,
,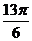 ],取
],取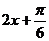 =
=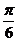 、
、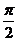 、
、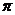 、
、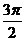 、2
、2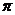 、
、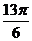 六个点,具体列表如下:
六个点,具体列表如下:
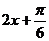 |
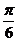 |
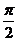 |
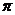 |
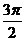 |
2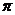 |
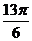 |
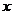 |
0 |
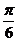 |
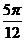 |
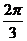 |
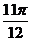 |
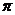 |
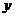 |
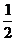 |
1 |
0 |
-1 |
0 |
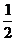 |
描点、作图略。不难看出直线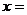
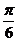 、
、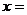
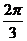 都不是函数的对称轴,点(
都不是函数的对称轴,点(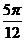 ,0)、(
,0)、(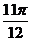 ,0)也都不是函数图象的对称中心,因为定义域不关于它们对称,所以无对称轴、对称中心。
,0)也都不是函数图象的对称中心,因为定义域不关于它们对称,所以无对称轴、对称中心。
[举例2] 已知函数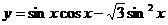 ,(1)指出函数的对称轴、对称中心;
,(1)指出函数的对称轴、对称中心;
(2)指出函数的单调递增区间;(3)函数在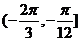 上的最大、最小值,并指出取得最大、最小值时的x的值。
上的最大、最小值,并指出取得最大、最小值时的x的值。
解析: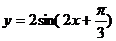 -
-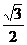 ,(1)对称轴:由
,(1)对称轴:由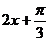 =
=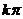 +
+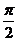 得
得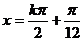 ,
,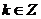 ;
;
对称中心:由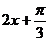 =
=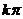 得
得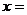
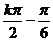 ,∴函数图象的对称中心为(
,∴函数图象的对称中心为(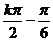 ,-
,-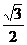 )
)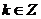 。(2)由
。(2)由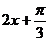 ∈[2
∈[2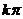 -
-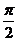 ,2
,2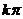 +
+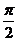 ]得
]得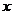 ∈[
∈[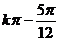 ,
,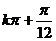 ],
],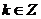 ,
,
∴[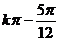 ,
,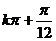 ],
],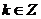 。(3)将
。(3)将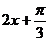 视为一个角
视为一个角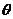 ,∵
,∵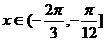
∴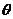 ∈
∈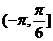 ,画函数
,画函数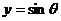 的草图,观察
的草图,观察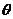 ∈
∈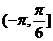 时函数值的范围为[-1,
时函数值的范围为[-1,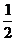 ],当且仅当
],当且仅当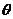 =
=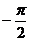 时
时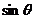 取得最小值-1,
取得最小值-1,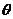 =
=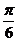 时
时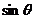 取得最大值
取得最大值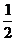 ;即
;即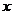 =
=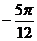 时原函数最小值-2-
时原函数最小值-2-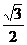 ,
,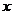 =
=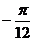 时原函数最大值1-
时原函数最大值1-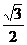 。
。
[巩固] [巩固]有以下四个命题:①函数f(x)=sin(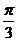 -2x)的一个增区间是[
-2x)的一个增区间是[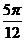 ,
,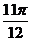 ];②若函数f(x)=sin(
];②若函数f(x)=sin(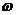 x+
x+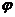 )为奇函数,则
)为奇函数,则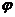 为
为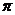 的整数倍;③对于函数f(x)=tg(2x+
的整数倍;③对于函数f(x)=tg(2x+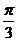 ),若f(x1)=f(x2),则x1-x2必是
),若f(x1)=f(x2),则x1-x2必是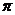 的整数倍;④函数y=2sin(2x+
的整数倍;④函数y=2sin(2x+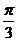 )的图像关于点(
)的图像关于点(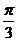 ,0)对称。
,0)对称。
其中正确的命题是 (填上正确命题的序号)
[迁移] 函数f(x)=2sin2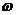 x+
x+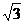 sin2
sin2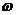 x-1 (
x-1 ( 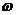 >0)
>0)
① 若对任意x∈R恒有f(x1)≤f(x)≤f(x2),求|x1-x2|的最小值;
② 若对任意x∈R恒f(x)≤f(1),试判断f(x+1)的奇偶性;
③
若f(x)在[0,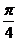 ]上是单调函数,求整数
]上是单调函数,求整数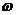 的值;
的值;
1.研究一个含三角式的函数的性质时一般先将函数化为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式。[注意]:函数y=|Asin(ωx+φ)|的周期是函数y=Asin(ωx+φ)周期的一半。
[举例]函数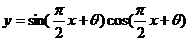 在
在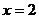 时有最大值,则
时有最大值,则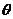 的一个值是,
的一个值是,
A、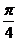 B、
B、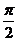 C、
C、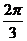 D、
D、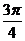
解析:原函数可变为: ,它在
,它在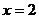 时有最大值,即
时有最大值,即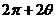 =2k
=2k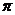 +
+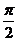
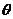 =(k-1)
=(k-1)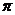 +
+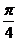 ,k∈Z,选A。(万不可分别去研究
,k∈Z,选A。(万不可分别去研究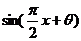 和
和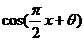 的最大值)。
的最大值)。
[巩固] ①函数y=sin2xcos2x的最小正周期是 ;
②函数y=tanx―cotx的周期为 ;③函数y=|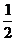 +sim
+sim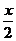 |的周期为 。
|的周期为 。
22.给题为“关注国计民生”的文章写一开头,要求:写三句话,要扣住题目,要具有文章开头的特点,三句话都要恰当地使用比喻的修辞手法,同时三句话还要构成排比。(6分)
答:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com