
13. 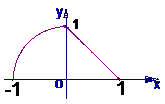 解题探究:因函数
解题探究:因函数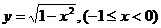 表示圆
表示圆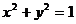 在第二象限的一部分,而函数
在第二象限的一部分,而函数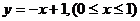 表示第一象限内的一条线段,通过旋转,组成半球与圆锥体的结合体,所以本题要利用球的表面积公式
表示第一象限内的一条线段,通过旋转,组成半球与圆锥体的结合体,所以本题要利用球的表面积公式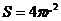 和圆锥的侧面积公式
和圆锥的侧面积公式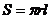 .
.
解析: y=f(x)=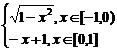 的图象如图所示 y=f(x)的曲线绕x轴旋转一周所得几何体是由一个半径为1的半球及底面半径和高均为1的圆锥体组成,从而其表面积为
的图象如图所示 y=f(x)的曲线绕x轴旋转一周所得几何体是由一个半径为1的半球及底面半径和高均为1的圆锥体组成,从而其表面积为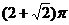 。
。
延伸拓展:将函数图象与立体几何结合在一起,是一个不错的题型,如2007年上海市高考第21题是:已知半椭圆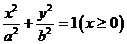 与半椭圆
与半椭圆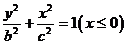 组成的曲线称为“果圆”,………。
组成的曲线称为“果圆”,………。
12. 解题探究:本题流程图表示一个分段函数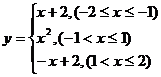 ,对于特殊方程,常用图象来观察解的情形。
,对于特殊方程,常用图象来观察解的情形。
解析:分别作出函数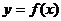 和
和 的图象,观察可知,有五个交点(包括原点),所以共有五个解。
的图象,观察可知,有五个交点(包括原点),所以共有五个解。
高考预测:有关方程解的个数问题,是近年高考的热点问题,如07年安徽高考题:定义在R上的函数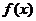
既是奇函数,又是周期函数,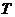 是它的一个正周期.若将方程
是它的一个正周期.若将方程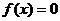 在闭区间
在闭区间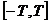 上的根的个
上的根的个
数记为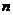 ,则
,则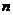 可能为 A.0 B.1 C.3 D.5 (参考答案:D)
可能为 A.0 B.1 C.3 D.5 (参考答案:D)
11. 解题探究:本题考查基本不等式、圆、直线方程等相关知识,其中整体代换是解题技巧,数形结合是解题思想。
解析:因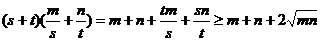 ,
,
所以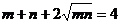 ,从而
,从而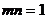 ,得
,得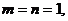 得点(1,1),而已知圆的圆心为(2,2),所求之弦的斜率为-1,从而弦方程为
得点(1,1),而已知圆的圆心为(2,2),所求之弦的斜率为-1,从而弦方程为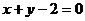 .
.
点评:本题涉及考试说明中的3个C级要求,是一道在知识交汇处命制的好题.在填空题中作为具有一定区分度的试题出现在后几题中,应沉着应试,冷静思考,逐步求解。
10. 解题探究:学会归纳猜想的数学思想,培养会举反例的严谨思维,寻找恰当的数据来说明结论的错误性。本题数列中相邻两数之差依次为2,4,6,8,所以利用等差数列的求和公式解决问题。.
解析: 根据题意知通项公式是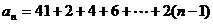
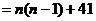 ,
,
取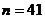 得
得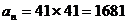 显然不是质数。
显然不是质数。
9. 解题探究:掌握简易逻辑的有关知识,学会数形结合的数学思想,理解二次方程与二次函数之间的关系,一元二次方程有一正根和一负根的充要条件是二次函数的图象与y轴相交于负半轴;而二次函数的图象与x轴有公共点的充要条件是二次方程有根,即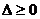 。
。
解析: 由命题p 得: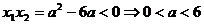 ;由命题q得:
;由命题q得: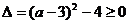 ,
,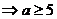 或
或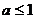 ;根据题意知命题p与命题q一真一假,当命题p真且命题q假时,
;根据题意知命题p与命题q一真一假,当命题p真且命题q假时,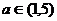 ;当命题q真且命题p假时,
;当命题q真且命题p假时,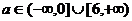 ,综上所述:
,综上所述: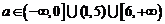
8. [解析探究]本题考查统计与概率的基础知识,分层抽样的方法实质是按比例分配兴趣小组中男、女同学的人数,从而过枚举写出基本事件的总数以及事件A发生的个数,利用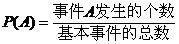 这一公式求 “恰有一名女同学”的概率.
这一公式求 “恰有一名女同学”的概率.
解析:显然男、女同学分别有3人和1人,将他们分别记为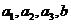 ,则选取两名同学的基本事件有
,则选取两名同学的基本事件有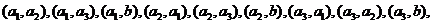
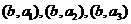 共
共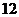 种,其中有一名女同学的有
种,其中有一名女同学的有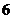 种,
种,
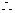 选出的两名同学中恰有一名女同学的概率为
选出的两名同学中恰有一名女同学的概率为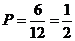
高考预测:有关涉及必修3的统计概率题,在福建省的高考试题中通常作为第一大解答题出现,值得同学们注意.
7. 解题探究:本题考查简单的函数导数知识,考查归纳猜想的数学思想,通过前几项的运算,寻找规律,解决问题.
解析:由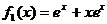 ,
,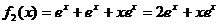 以此类推,
以此类推,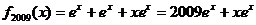 。
。
6. 解题探究:考查立体几何的有关知识,回忆线线、线面位置关系,即可判断正确与否. 命题①中直线m可能也在平面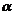 内;同理命题④中直线
内;同理命题④中直线 可能与平面
可能与平面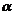 相交。
相交。
解析: 正确的命题序号是②③。
5.解题探究:本题将分段函数与数列有机地结合在一起,考查分类讨论的数学思想,只要审清题意,通过必要的代换,就能求之.
解析:因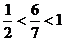 ,所以
,所以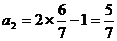 ,
,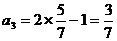 ,从而
,从而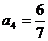 ,即该数列是循环数列,周期是3,所以
,即该数列是循环数列,周期是3,所以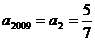 .
.
4. 解题探究:本题考查数形结合的数学思想,作出可行域,利用目标函数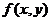 的几何意义求之.
的几何意义求之.
解析:约束条件是一个三角形区域,而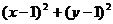 表示以(1,1)为圆心的圆,从而最小值是点(1,1)到直线
表示以(1,1)为圆心的圆,从而最小值是点(1,1)到直线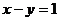 的距离的平方,即
的距离的平方,即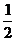 ,最大值为点(1,1)到点(2,0)的距离的平方,即为2.从而取值范围是
,最大值为点(1,1)到点(2,0)的距离的平方,即为2.从而取值范围是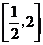 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com