
5.研究椭圆上一点与两焦点组成的三角形(焦点三角形)问题时,常用椭圆定义及正、余弦定理。
[举例]已知焦点在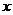 轴上的椭圆
轴上的椭圆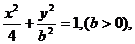 F1,F2是它的两个焦点,若椭圆上存在点P,使得
F1,F2是它的两个焦点,若椭圆上存在点P,使得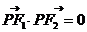 ,则
,则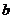 的取值范围是
。
的取值范围是
。
解析:思路一:先证一个结论:若B为椭圆短轴端点,则∠F1PF2≤∠F1BF2。记∠F1PF2=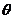 ,
,
|PF1|=r1, |PF2|=r2,cos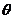 =
=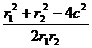 =
=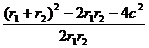 =
=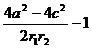
又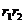 ≤(
≤(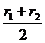 )2=
)2=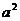 ,∴cos
,∴cos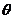 ≥
≥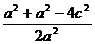 =cos∠F1BF2,当且仅当r1=r2时等号成立,
=cos∠F1BF2,当且仅当r1=r2时等号成立,
即∠F1PF2≤∠F1BF2。题中椭圆上存在点P,使得∠F1PF2=900,当且仅当∠F1BF2≥900,即
cos∠F1BO≤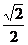
 b≤
b≤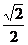 a=
a=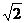 ,∴b∈(0,
,∴b∈(0, 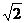
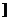 .思路二:用勾股定理:r1+r2=2a
①
.思路二:用勾股定理:r1+r2=2a
①
r12+r22=4c2 ②,由①②得:2r1r2=4b2,又2r1r2≤r12+r22 ∴b2≤c2=4-b2 即b∈(0, 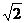
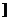 .
.
思路三:用向量的坐标运算:记P(x0,y0),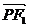 =(-c-x0,-y0),
=(-c-x0,-y0), 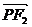 =(c-x0,-y0),
=(c-x0,-y0),
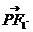
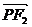 =c2-x02+y02=0
=c2-x02+y02=0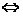 (b2+4)x02=4(c2-b2),注意到:0≤x02≤4,∴0≤4(c2-b2)≤4(b2+4)
(b2+4)x02=4(c2-b2),注意到:0≤x02≤4,∴0≤4(c2-b2)≤4(b2+4)
即0≤4-2b2≤b2+4,得b∈(0, 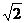
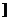 .
.
[巩固1]椭圆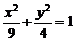 的焦点为
的焦点为 、
、 ,点P为其上的动点,当
,点P为其上的动点,当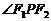 为钝角时,点P横坐标的取值范围是________。
为钝角时,点P横坐标的取值范围是________。
[巩固2]已知P是椭圆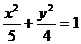 上一点,F1和F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
上一点,F1和F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
A.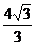 B.
B.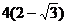 C.
C.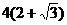 D.4
D.4
4.研究椭圆上的点到其焦点的距离问题时,往往用定义;会推导并记住椭圆的焦半径公式。
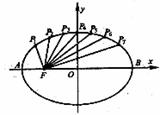 [举例1] 如图把椭圆
[举例1] 如图把椭圆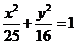 的长轴AB分成8分,过
的长轴AB分成8分,过
每个分点作x轴的垂线交椭圆的上半部分于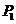 ,
,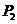 ,……
,……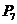
七个点,F是椭圆的一个焦点,则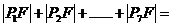 ____________.
____________.
解析:P1与P7,P2与P6,P3与P5关于y轴对称,P4在y轴上,
记椭圆的另一个焦点为F/,则|P7F|=|P1F/|,|P6F|=|P2F/|,|P5F|=|P3F/|,
于是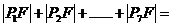 |P1F|+|P1F/|+|P2F|+|P2F/|+|P3F|+|P3F/|+|P4F|=7a=35.
|P1F|+|P1F/|+|P2F|+|P2F/|+|P3F|+|P3F/|+|P4F|=7a=35.
[举例2] 已知A、B是椭圆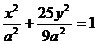 上的两点,F2是椭圆的右焦点,如果
上的两点,F2是椭圆的右焦点,如果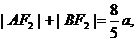 AB的中点到椭圆左准线距离为
AB的中点到椭圆左准线距离为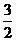 ,则椭圆的方程 .
,则椭圆的方程 .
解析: 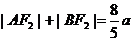
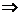
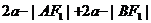 =
=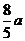
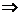
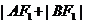 =
=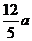 ,
,
记AB的中点为M ,A、B、M在椭圆左准线上的射影分别为A1、B1,M1,由椭圆第二定义知:|AF1|=e|AA1|,|BF1|=e|BB1|,于是有:e(|AA1|+|BB1|)=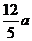 ,而e=
,而e=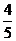
∴|AA1|+|BB1|=3a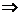 2|MM1|=3a,又|MM1|=
2|MM1|=3a,又|MM1|=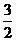 ,得a=1,故椭圆方程为
,得a=1,故椭圆方程为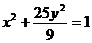 。
。
[巩固1] 椭圆的两焦点为F1,F2,以F1F2为一边的正三角形的另两条边均被椭圆平分,则椭圆的离心率为 。
[巩固2]已知F1、F2是椭圆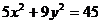 的左右焦点,点
的左右焦点,点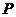 是此椭圆上的一个动点,
是此椭圆上的一个动点,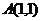 为一个定点,则
为一个定点,则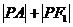 的最大值为
,
的最大值为
,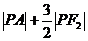 的最小值为
。
的最小值为
。
[提高] 过椭圆左焦点F且斜率为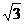 的直线交椭圆于A、B两点,若|FA|=2|FB|,则椭圆的离心率e=_____
的直线交椭圆于A、B两点,若|FA|=2|FB|,则椭圆的离心率e=_____
3.圆锥曲线的定义是求轨迹方程的重要载体之一。
[举例1]已知⊙Q:(x-1)2+y2=16,动⊙M过定点P(-1,0)且与⊙Q相切,则M点的轨迹方程是:
。
解析:P(-1,0)在⊙Q内,故⊙M与⊙Q内切,记:M(x,y),⊙M的半径是为r,则:
|MQ|=4-r,又⊙M过点P,∴|MP|=r,于是有:|MQ|=4-|MP|,即|MQ|+|MP|=4,可见M点的轨迹是以P、Q为焦点(c=1)的椭圆,a=2。
[举例2] 若动点P(x,y)满足|x+2y-3|=5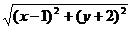 ,则P点的轨迹是:
,则P点的轨迹是:
A.圆 B、椭圆 C、双曲线 D、抛物线
解析:等式两边平方,化简方程是最容易想到的,但不可行,一方面运算量很大,另一方面是平方、展开后方程中会出现xy项,这就给我们判断曲线类型带来了麻烦。但是,仔细观察方程后,就会发现等式左边很“象”是点到直线的距离,而等式右边则是两点间的距离的5倍;为了让等式左边变成点到直线的距离,可以两边同除以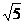 ,于是有:
,于是有:
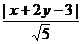 =
=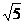
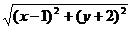 ,这就已经很容易联想到圆锥曲线的第二定义了,
,这就已经很容易联想到圆锥曲线的第二定义了,
只需将方程再变形为: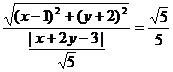 ,即动点P(x,y)到定点A(1,2)与到定直线x+2y-3=0的距离之比为
,即动点P(x,y)到定点A(1,2)与到定直线x+2y-3=0的距离之比为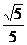 ,∴其轨迹为椭圆。
,∴其轨迹为椭圆。
[巩固1] 已知圆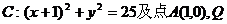 为圆上一点,AQ的垂直平分线交CQ于M,则点M的轨迹方程为
.
为圆上一点,AQ的垂直平分线交CQ于M,则点M的轨迹方程为
.
[巩固2]设x、y∈R,在直角坐标平面内,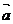 =(x,y+2),
=(x,y+2),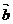 =(x,y-2),且|
=(x,y-2),且|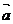 |+|
|+|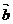 |=8,则点
|=8,则点
M(x,y)的轨迹方程为 。
[提高]已知A(0,7),B(O,-7),C(12,2),以C为一个焦点作过A、B的椭圆,则椭圆的另一焦点的轨迹方程为 。
[迁移] P为直线x-y+2=0上任一点,一椭圆的两焦点为F1(-1,0)、F2(1,0),则椭圆过P点且长轴最短时的方程为 。
2.椭圆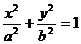 关于x轴、y轴、原点对称;P(x,y)是椭圆上一点,则|x|≤a,|y|≤b,
关于x轴、y轴、原点对称;P(x,y)是椭圆上一点,则|x|≤a,|y|≤b,
a-c≤|PF|≤a+c,(其中F是椭圆的一个焦点),椭圆的焦点到短轴端点的距离为a,椭圆的焦准距为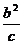 ,椭圆的通经(过焦点且垂直于长轴的弦)长为2
,椭圆的通经(过焦点且垂直于长轴的弦)长为2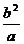 ,通经是过焦点最短的弦。
,通经是过焦点最短的弦。
[举例1] 已知椭圆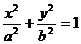 (
(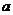 >0,
>0,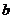 >0)的左焦点为F,右顶点为A,上顶点为B,若
>0)的左焦点为F,右顶点为A,上顶点为B,若
BF⊥BA,则称其为“优美椭圆”,那么“优美椭圆”的离心率为 。
解析:|AB|2=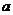 2+
2+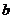 2,|BF|=
2,|BF|=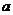 ,|FA|=
,|FA|=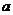 +
+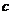 ,在Rt⊿ABF中,(
,在Rt⊿ABF中,(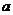 +
+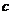 )2=
)2=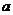 2+
2+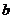 2+
2+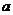 2
2
化简得: 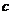 2+
2+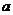
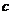 -
-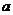 2=0,等式两边同除以
2=0,等式两边同除以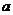 2得:
2得: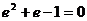 ,解得:
,解得: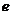 =
=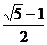 。
。
注:关于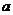 ,
,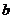 ,
,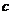 的齐次方程是“孕育”离心率的温床。
的齐次方程是“孕育”离心率的温床。
[举例2] 已知椭圆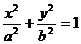 (
(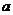 >0,
>0,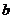 >0)的离心率为
>0)的离心率为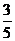 ,若将这个椭圆绕着它的右焦点按逆时针方向旋转
,若将这个椭圆绕着它的右焦点按逆时针方向旋转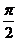 后,所得的新的椭圆的一条准线的方程为
后,所得的新的椭圆的一条准线的方程为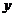 =
=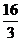 ,则原来椭圆的方程是
。
,则原来椭圆的方程是
。
解析:原来椭圆的右焦点为新椭圆的上焦点,在x轴上,直线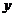 =
=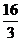 为新椭圆的上准线,故新椭圆的焦准距为
为新椭圆的上准线,故新椭圆的焦准距为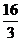 ,∴原来椭圆的焦准距也为
,∴原来椭圆的焦准距也为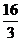 ,于是有:
,于是有: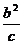 =
=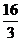 ①,
①,
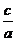 =
=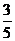 ②,由①②解得:
②,由①②解得: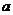 =5,
=5,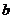 =3。
=3。
[巩固1]一椭圆的四个顶点为A1,A2,B1,B2,以椭圆的中心为圆心的圆过椭圆的焦点,的椭圆的离心率为 。
[巩固2] 在给定椭圆中,过焦点且垂直于长轴的弦长为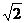 ,焦点到相应准线的距离为1,则该椭圆的离心率为
,焦点到相应准线的距离为1,则该椭圆的离心率为
(A)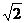 (B)
(B)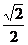 (C)
(C) 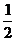 (D)
(D)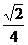
[迁移]椭圆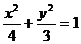 上有n个不同的点P1,P2,P3,…,Pn,椭圆的右焦点F,数列{| PnF|}
上有n个不同的点P1,P2,P3,…,Pn,椭圆的右焦点F,数列{| PnF|}
是公差大于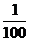 的等差数列,则n的最大值为
( )
的等差数列,则n的最大值为
( )
A.198 B.199 C.200 D.201
1.方程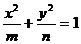 表示椭圆
表示椭圆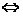
 >0,
>0, >0,且
>0,且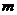 ≠
≠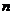 ;
;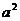 是
是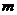 ,
,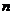 中之较大者,焦点的位置也取决于
中之较大者,焦点的位置也取决于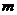 ,
,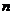 的大小。
的大小。
[举例] 椭圆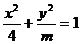 的离心率为
的离心率为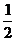 ,则
,则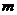 =
=
解析:方程中4和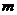 哪个大哪个就是
哪个大哪个就是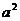 ,因此要讨论;(ⅰ)若0<
,因此要讨论;(ⅰ)若0<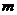 <4,则
<4,则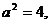
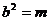 ,∴
,∴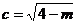 ,∴
,∴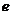 =
=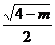 =
=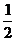 ,得
,得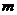 =3;(ⅱ)
=3;(ⅱ)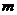 >4,则
>4,则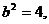
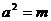 ,∴
,∴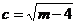 ,∴
,∴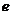 =
=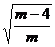 =
=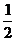 ,得
,得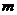 =
=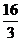 ;综上:
;综上: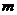 =3或
=3或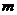 =
=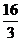 。
。
[巩固]若方程:x2+ay2=a2 表示长轴长是短轴长的2倍的椭圆,则a的允许值的个数是
A 1个 B .2个 C.4个 D.无数个
本题为选做题,考生须从所给(一)(二)两题中任选一题作答;不能全选。
18.根据“人才派遣”示意图的提示,填写下面一段话中空缺的内容。
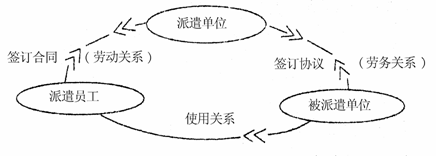
人才派遣亦称人才租赁,它是由 , ,从而使被派遣单位与派遣员工之间建立起使用关系的一种现代人力资源管理的新型用人形式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com