
2.已知复数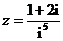 ,则它的共轭复数
,则它的共轭复数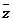 等于
( )
等于
( )
A.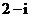 B.
B.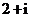 C.
C.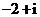 D.
D.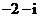
1.已知全集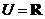 ,集合
,集合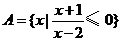 ,则集合
,则集合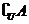 等于
( )
等于
( )
A.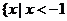 或
或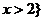 B.
B.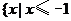 或
或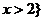
C.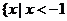 或
或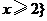 D.
D.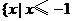 或
或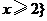
22.已知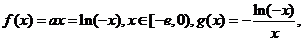 其中
其中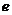 是自然常数,
是自然常数,
(Ⅰ)讨论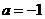 时,
时, 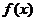 的单调性、极值;
的单调性、极值;
(Ⅱ)求证:在(1)的条件下,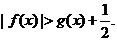
(Ⅲ)是否存在实数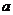 ,使
,使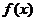 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出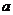 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
解:(Ⅰ)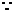
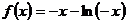
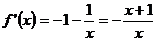
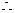 当
当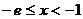 时,
时,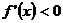 ,此时
,此时 为单调递减
为单调递减
当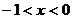 时,
时,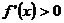 ,此时
,此时 为单调递增
为单调递增
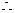
 的极小值为
的极小值为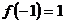
(Ⅱ)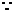
 的极小值,即
的极小值,即 在
在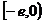 的最小值为1
的最小值为1
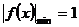 令
令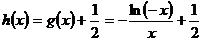
又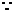
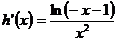 当
当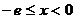 时
时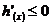
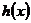 在
在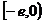 上单调递减
上单调递减
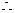
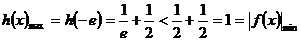
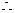 当
当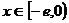 时,
时,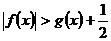
(Ⅲ)假设存在实数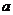 ,使
,使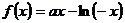 有最小值3,
有最小值3,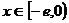
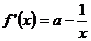
①当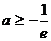 时,由于
时,由于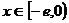 ,则
,则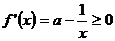
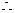 函数
函数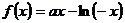 是
是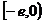 上的增函数
上的增函数
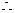
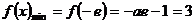
解得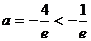 (舍去)
(舍去)
②当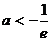 时,则当
时,则当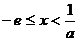 时,
时,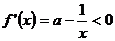
此时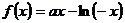 是减函数
是减函数
当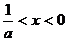 时,
时,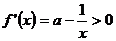 ,此时
,此时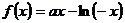 是增函数
是增函数
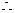
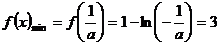
解得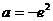 ,由①、②知,存在实数
,由①、②知,存在实数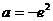 ,使得当
,使得当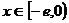 时
时 有最小值3
有最小值3
21.(本小题满分12分)
设椭圆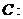
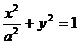 (
(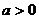 )的两个焦点是
)的两个焦点是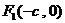 和
和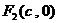 (
(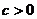 ),且椭圆
),且椭圆 与圆
与圆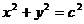 有公共点.(Ⅰ)求
有公共点.(Ⅰ)求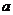 的取值范围;
的取值范围;
(Ⅱ)若椭圆上的点到焦点的最短距离为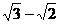 ,求椭圆的方程;
,求椭圆的方程;
(Ⅲ)对(2)中的椭圆 ,直线
,直线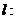
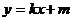 (
(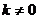 )与
)与 交于不同的
交于不同的
两点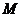 、
、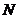 ,若线段
,若线段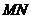 的垂直平分线恒过点
的垂直平分线恒过点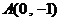 ,求实数
,求实数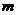 的取值范围.
的取值范围.
解:(Ⅰ)由已知,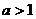 ,
,
∴ 方程组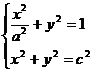 有实数解,从而
有实数解,从而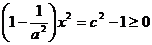 , 故
, 故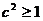 ,所以
,所以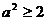 ,即
,即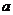 的取值范围是
的取值范围是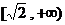 .
.
(Ⅱ)设椭圆上的点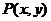 到一个焦点
到一个焦点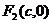 的距离为
的距离为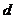 ,
,
则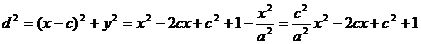
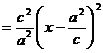 (
(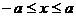 ). ∵
). ∵ 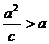 ,∴ 当
,∴ 当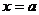 时,
时,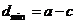 ,
,
于是,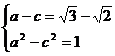 ,解得
,解得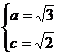 .
.
∴ 所求椭圆方程为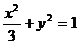 .
.
(Ⅲ)由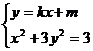 得
得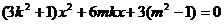 (*)
(*)
∵ 直线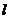 与椭圆交于不同两点, ∴ △
与椭圆交于不同两点, ∴ △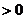 ,即
,即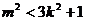 .①
.①
设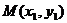 、
、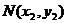 ,则
,则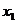 、
、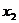 是方程(*)的两个实数解,
是方程(*)的两个实数解,
∴ 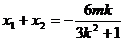 ,∴ 线段
,∴ 线段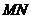 的中点为
的中点为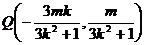 ,
,
又∵ 线段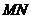 的垂直平分线恒过点
的垂直平分线恒过点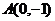 ,∴
,∴ 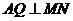 ,
,
即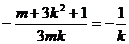 ,即
,即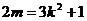 (k
(k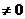 ) ②
) ②
由①,②得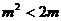 ,
,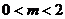 ,又由②得
,又由②得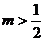 ,
,
∴ 实数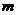 的取值范围是
的取值范围是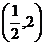 .
.
20.(本小题满分12分)
曲线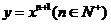 在点
在点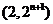 处的切线与x轴的交点的横坐标为
处的切线与x轴的交点的横坐标为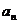 .
.
(Ⅰ)求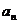 ;
;
(Ⅱ)设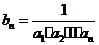 ,求数列{
,求数列{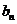 }的前n项和
}的前n项和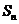 .
.
解:∵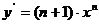 ,∴直线的方程为
,∴直线的方程为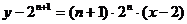 ,
,
令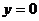 ,得
,得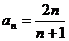 .
.
(Ⅱ)∵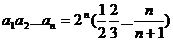 ,∴
,∴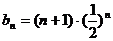
∴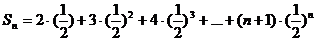
∴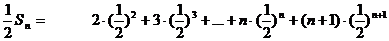
∴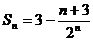
19. (本小题满分12分)
已知四棱锥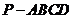 的
的 底面
底面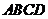 是菱形;
是菱形;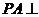 平面
平面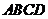 ,
,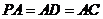 ,
,
点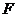 为
为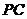 的中点.
的中点.
(Ⅰ)求证: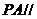 平面
平面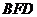 ;
;
(Ⅱ)求二面角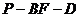 的大小.
的大小.
(Ⅰ)证明: 连结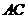 ,
,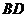 与
与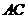 交于点
交于点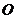 ,连结
,连结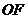 .
. 
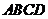 是菱形, ∴
是菱形, ∴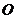 是
是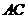 的中点.
的中点.  点
点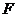 为
为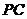 的中点, ∴
的中点, ∴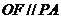 .
. 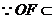 平面
平面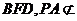 平面
平面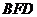 , ∴
, ∴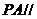 平面
平面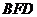 .
.
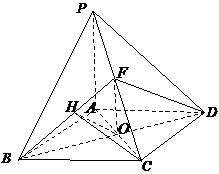 (Ⅱ)解法一:
(Ⅱ)解法一:
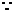
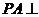 平面
平面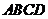 ,
,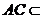 平面
平面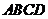 ,∴
,∴ 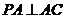 .
.
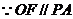 ,∴
,∴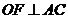 .
. 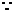
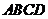 是菱形, ∴
是菱形, ∴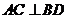 .
.
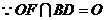 ,
,
∴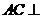 平面
平面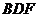 .
.
作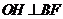 ,垂足为
,垂足为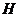 ,连接
,连接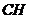 ,则
,则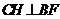 ,
,
所以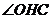 为二面角
为二面角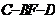 的平面角.
的平面角.
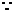
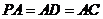 ,∴
,∴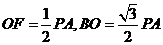 ,
,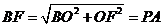 .
.
在Rt△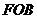 中,
中,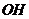 =
=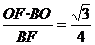
 ,∴
,∴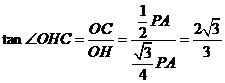 .
.
∴二面角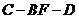 的大小为
的大小为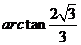
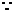 二面角
二面角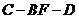 的平面角与二面角
的平面角与二面角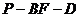 的平面角互补
的平面角互补
∴二面角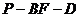 的大小为
的大小为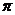 —
—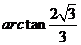
解法二:如图,以点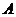 为坐标原点,线段
为坐标原点,线段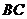 的垂直平分线所在直线为
的垂直平分线所在直线为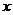 轴,
轴,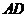 所在直线为
所在直线为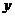 轴,
轴,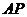 所在直线为
所在直线为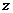 轴,建立空间直角坐标系,令
轴,建立空间直角坐标系,令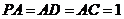 ,
,
则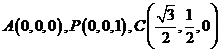 ,
,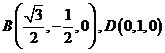 ,
,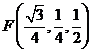 .
.
 ∴
∴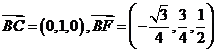 .设平面
.设平面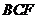 的一个法向量为
的一个法向量为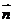
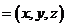 ,
,
由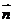
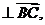
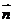
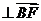 ,得
,得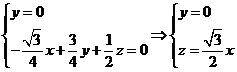 ,
,
令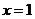 ,则
,则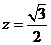 ,∴
,∴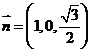 .
.
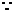
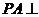 平面
平面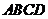 ,
,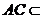 平面
平面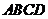 ,
,
∴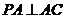 .
.
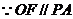 ,∴
,∴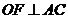 .
.
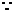
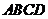 是菱形,∴
是菱形,∴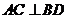 .
.
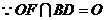 ,∴
,∴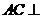 平面
平面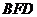 .
.
∴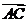 是平面
是平面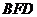 的一个法向量,
的一个法向量,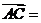
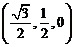 .
.
∴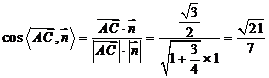 ,
,
∴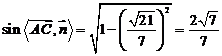 ,∴
,∴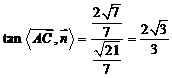 . 13分
. 13分
∴二面角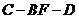 的大小为
的大小为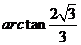
∴二面角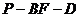 的大小为
的大小为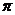 —
—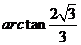 。
。
18.(本小题满分12分)
甲袋和乙袋中都装有大小相同的红球和白球,已知甲袋中共有m个球,乙袋中共有2m个球,从甲袋中摸出一个球为红球的概率为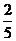 ,从乙袋中摸出一个球为红球的概率为
,从乙袋中摸出一个球为红球的概率为 .
.
(I) 若m=10,求甲袋中红球的个数;
(II)
若将甲、乙两袋中的球装在一起后,从中摸出一个红球的概率是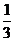 ,求出
,求出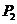 的值;
的值;
(III)
设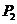 =
=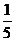 ,若从甲、乙两袋中各自有放回的摸球,每次摸出一个球,并且从甲袋中摸一次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和期望.
,若从甲、乙两袋中各自有放回的摸球,每次摸出一个球,并且从甲袋中摸一次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和期望.
解:(I)设甲袋中红球的个数为x,依题意得 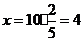 .
.
(II)由已知得: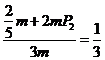 ,解得
,解得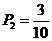 .
.
(III)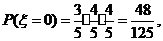
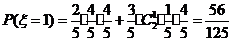
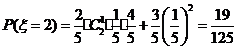
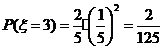
|
_ξ |
0 |
1 |
2 |
3 |
|
p |
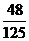 |
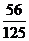 |
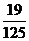 |
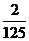 |
所以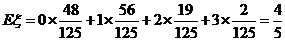
17.(本小题满分10分)
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;
|
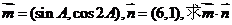 的最大值。
的最大值。
(I)∵(2a-c)cosB=bcosC,∴(2sinA-sinC)cosB=sinBcosC
即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA.∵0<A<π,∴sinA≠0. ∴cosB=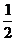 .
.
∵0<B<π,∴B=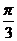 .
.
(II)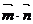 =6sinA+cos2A.=-2sin2A+6sinA+1,A∈(0,
=6sinA+cos2A.=-2sin2A+6sinA+1,A∈(0,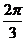 )设sinA=t,则t∈
)设sinA=t,则t∈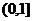 .
.
则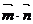 =-2t2+6t+1=-2(t-
=-2t2+6t+1=-2(t-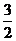 )2+
)2+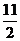 ,t∈
,t∈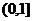 .∴t=1时,
.∴t=1时,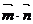 取最大值.5
取最大值.5
16.已知方程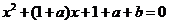 的两个实根
的两个实根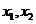 ,满足0﹤
,满足0﹤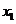 ﹤1﹤
﹤1﹤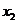 ,则
,则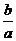 的取值范围是_
的取值范围是_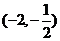 .
.
15.已知双曲线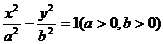 的右顶点到其渐近线的距离不大于
的右顶点到其渐近线的距离不大于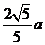 ,其离心率e的取值范围为
,其离心率e的取值范围为 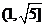 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com