
5、在2010年第21届温哥华冬奥会上,中国名将( )夺得花样滑冰双人滑项目金牌。这是中国花样滑冰在冬奥会上获得的首枚金牌,也是自1960年冬奥会以来第一对获得这个项目金牌的非俄罗斯(前苏联)选手。
A.庞清/佟健 B.申雪/赵宏博
C.张丹/张昊 D.王濛/刘佳宇
4、2009年12月29日,中共中央政治局召开会议研究部署党风廉政建设和反腐败工作。会议审议并通过《中国共产党党员领导干部( )若干准则》。
A.反腐倡廉 B.行为规范
C.密切联系群众 D.廉洁从政
3、2009年11月4日,上海市人民政府新闻办公室授权宣布:上海( )项目申请报告已获国家有关部门核准,将在浦东新区兴建。
A.金融创新 B.浦东机场二期工程
C.迪士尼 D.科技乐园
1、国家统计局2010年1月21日发布数据显示,2009年我国GDP同比增长( ),我国经济“保八”成功,领先全球复苏。
A.8% B.8.2% C.8.5% D.8.7%
21.(本小题满分13分)
已知函数f(x)=ex+2x2-3x
(工)求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求证函数f(x)在区间[0,1)上存在唯一的极值点;
(Ⅲ)当x≥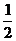 时,若关于x的不等式f(x)≥
时,若关于x的不等式f(x)≥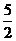 x2+(a-3)x+1恒成立,试求实数
x2+(a-3)x+1恒成立,试求实数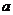
的取值范围.
(Ⅰ)f'(x)=ex+4x-3,则f'(1)=e+1,............1分
又f(1)=e-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为
y-e+1=(e+1)(x-1),且(e+1)x-y-2=0............3分
(Ⅱ)∵f'(0)=e0-3=-2<0,f'(1)=e+1>0,
∴f'(0)·f'(1)<0
令h(x)=f'(x)=ex+4x-3,
则h'(x)=ex+4>0,f'(x)在 [0,1]上单调递增,
∴.f'(x)在[0,1]上存在唯一零点,f(x)在[0,1]上存在唯一的极值点.……7分
(Ⅲ)由f(x)≥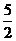 x2+(a-3)x+1得ex+2x2-3x≥
x2+(a-3)x+1得ex+2x2-3x≥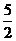 x2+(a-3)x+1
x2+(a-3)x+1
即ax≤ex-1/2 x2-1,∵x≥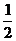 ,
,
∴a≤ 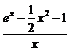 令g(x)=
令g(x)= 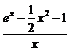 ,则g’(x)=
,则g’(x)= 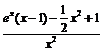
令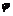 (x)=ex(x-1)-
(x)=ex(x-1)- 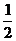 x2+1,则
x2+1,则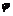 ’(x)=x(ex-1)
’(x)=x(ex-1)
∵x≥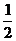 ,∴
,∴ ’(x)>0,∴
’(x)>0,∴ (x)在[
(x)在[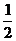 ,+∞)上单调递增,
,+∞)上单调递增,
∴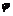 (x)≥
(x)≥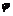 (
(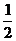 )=
)=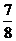 -
-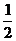
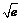 >0
>0
因此g’(x)>0 ,故g(x)在[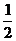 ,+∞)上单调递增,
,+∞)上单调递增,
则g(x)≥g(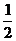 )
)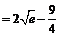 ∴a的取值范围是a≤2
∴a的取值范围是a≤2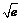 -
-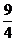 …………..13分
…………..13分
20.(本小题满分13分)
已知抛物线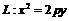 点
点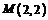 ,抛物线L上存在不同两点A、B满足
,抛物线L上存在不同两点A、B满足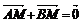
(1)求实数p 的取值范围;
(2)当p=2时,抛物线L上是否存在点C,使得经过A、B、C三点的的圆和抛物线L在点C处有相同的切线?请写出推理过程.
解:(1)解法1:不妨设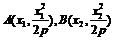 ,且x1<x2,
,且x1<x2,
∵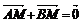 ,∴
,∴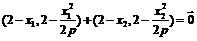 .
.
∴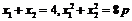 .………………………………………………………………3分
.………………………………………………………………3分
∵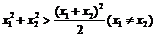 ,即8p>8,
,即8p>8,
∴p>1,即p的取值范围为(1, +∞).……………………………………………………5分
解法2:设A、B两点的坐标为A(x1, y1),B(x2,y2),且x1<x2.
∵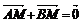 ,可得M为AB的中点,即
,可得M为AB的中点,即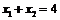 .
.
显然直线AB与x轴不垂直,设直线AB的方程为y – 2 = k(x – 2),
即y = kx + 2– 2k,…………………………………………………………………………3分
将y = kx + 2– 2k代入x2 = 2py中,得x2 –2pkx + 4(k –1)p = 0.
∴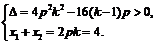
∴ p>1.
故p的取值范围为(1, +∞).……………………………………………………………5分
(2)当p = 2时,由(1)求得A、B的坐标分别为(0, 0)、(4,4)……………………6分
假设抛物线L上存在点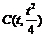 (t≠0且t≠4),使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.
(t≠0且t≠4),使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.
设经过A、B、C三点的圆的方程为x2 + y2 + Dx + Ey + F =0,
则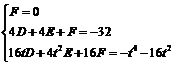
整理得t3 + 4(E + 4)t – 16(E + 8) = 0.①…………………………………………8分
∵函数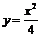 的导数为
的导数为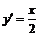 ,
,
∴抛物线L在点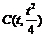 处的切线的斜率为
处的切线的斜率为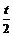 ,
,
∴经过A、B、C三点的圆N在点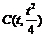 处的切线斜率为
处的切线斜率为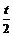 .
.
∵t≠0,∴直线NC的斜率存在.
∵圆心N的坐标为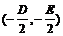 ,
,
∴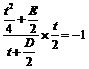 ,即t3 + 2(E + 4)t – 4(E + 8) = 0.②
,即t3 + 2(E + 4)t – 4(E + 8) = 0.②
∵t≠0,由①、②消去E,得t3 – 6t2 + 32 = 0……………………………………12分
即(t – 4)2(t + 2) =0. ∵t≠4,∴t = –2.
故满足题设的点C存在,其坐标为(–2,1).……………………………………13分
(也可以构造三次函数只证明存在性)
19.(本小题满分13分)
学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费为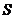 元,用电炉烧开水每吨开水费为
元,用电炉烧开水每吨开水费为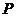 元,且
元,且
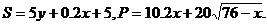
其中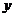 为每吨煤的价格,
为每吨煤的价格,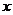 为每百度电的价格,如果用煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
为每百度电的价格,如果用煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
(1)如果两种方法烧水费用相同,试将每吨煤的价格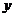 表示为每百度电的价格
表示为每百度电的价格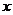 的函数;
的函数;
(2)如果每百度电的价格不低于60元,则用煤烧水时每吨煤的最高价是多少?
解:(1)由题意,得5y+0.2x+5=10.2x+20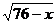 ,
,
即 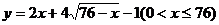 …………5分
…………5分
(2)因为用煤炉烧开水,所以S≤P,
得5y+0.2x+5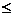 10.2x+20
10.2x+20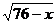 …………7分
…………7分
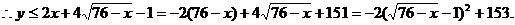
…………10分
∵ 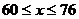 .∴
.∴ 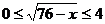 .
11分
.
11分
∴ 当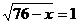 即
即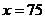 时,
时,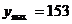 , …………12分
, …………12分
答:每吨煤的最高价为153元. ………13
18.(本题满分12分)已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=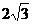 ,如图,O、H分别为AE,AB的中点,
,如图,O、H分别为AE,AB的中点,
(1)求证:平面AED⊥平面ABCD
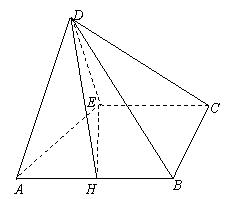 (2)求二面角O-DH-E的余弦值
(2)求二面角O-DH-E的余弦值
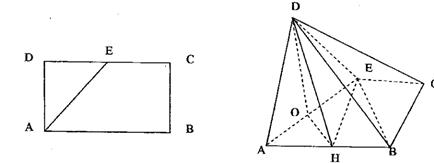
.解:(1)∵E为CD中点,O为AE中点∴DO⊥AE①
∵AB=2AD=4 ∴AE=BE=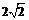 ∴EO=DO=
∴EO=DO=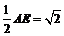
∴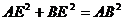 ∴AE⊥EB ∴BO=
∴AE⊥EB ∴BO=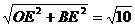
又∵BD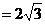 ∴
∴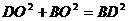 ∴
∴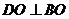 ②
②
由①②知DO⊥面ABCD
∴DO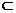 面ADE ∴面ADE⊥面ABCD……………………………………………6
面ADE ∴面ADE⊥面ABCD……………………………………………6
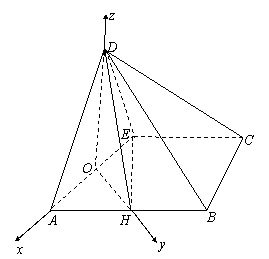 (2)如图,以O为坐标原点,OA、OH、OD所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则D(0,0,
(2)如图,以O为坐标原点,OA、OH、OD所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则D(0,0,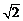 ),E(–
),E(–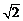 ,0,0),H(0,
,0,0),H(0,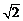 ,0),则
,0),则
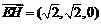 ,
,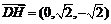 ,
,
设平面DEH的一个法向量为n1 = (x, y, z),则
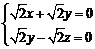 ,令z = 1,则y = 1,x
= –1,
,令z = 1,则y = 1,x
= –1,
N1 = (–1,1,1),n2 = (1,0,,0)为平面DOH的一个法向量,
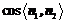 =
=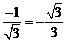 .
.
故二面角O-DH-E的平面角的余弦值为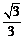 .………………………………12分
.………………………………12分
16.(本题满分12分)
设△ABC的内角A、B、C所对的边长分别为a、b、c,且
(1)试求tanA与tanB的关系;
(2)求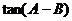 的最大值.
的最大值.
解:(1)在△ABC中,由正弦定理及
可得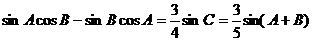 …………2分
…………2分
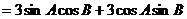
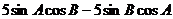
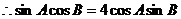
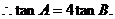 …………………………6分
…………………………6分
(2)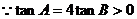
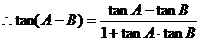
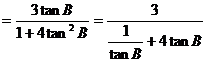 ………………8分
………………8分
 ……………………10分
……………………10分
当且仅当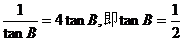 时取等号.
时取等号.
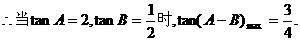 … 12分
… 12分
17(本题满分12分).10个实习小组在显微镜下实测一块矩形芯片,测得其长为29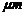 ,30
,30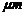 ,31
,31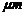 的小组分别有3个,5个,2个,测得其宽为19
的小组分别有3个,5个,2个,测得其宽为19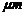 ,20
,20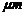 ,21
,21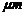 的小组分别有3个,4个,3个,设测量中矩形芯片的长与宽分别为随机变量
的小组分别有3个,4个,3个,设测量中矩形芯片的长与宽分别为随机变量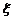 和
和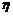 ,周长为
,周长为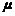 .
.
(Ⅰ)以表格形式,填写随机变量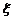 和
和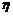 的分布律;
的分布律;
(Ⅱ)求周长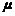 的分布列及期望.
的分布列及期望.
[解析](Ⅰ)
长度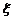 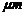 |
29 |
30 |
31 |
|
P |
0.3 |
0.5 |
0.2 |
…………………………………………………………………………………3
宽度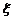 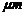 |
19 |
20 |
21 |
|
P |
0.3 |
0.4 |
0.3 |
……………………………………………………………………………………6
(Ⅱ)P(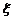 =96) = 0.3×0.3=0.09;
=96) = 0.3×0.3=0.09;
P(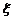 =98)= 0.3×0.4+0.5×0.3 =0.27;
=98)= 0.3×0.4+0.5×0.3 =0.27;
P(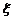 =100)= 0.5×0.4 + 0.2×0.3 + 0.3×0.3
= 0.35;
=100)= 0.5×0.4 + 0.2×0.3 + 0.3×0.3
= 0.35;
P(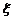 =102)= 0.2×0.4 + 0.5×0.3 = 0.35;
=102)= 0.2×0.4 + 0.5×0.3 = 0.35;
P(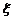 =104)= 0.2×0.3=0.06.………………………………………………………9
=104)= 0.2×0.3=0.06.………………………………………………………9
得周长分布律如下表所示:
周长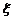 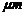 |
96 |
98 |
100 |
102 |
103 |
|
P |
0.09 |
0.27 |
0.35 |
0.23 |
0.06 |
………………………………………………….12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com