
5.影响火电厂分布的主要因素是 ( )
A.历史 B.经济 C.环境 D.交通
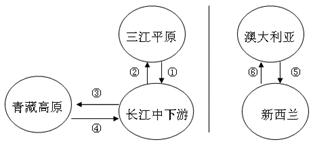
候鸟迁徙的一般规律是:越冬时,由温度较低的地区迁往温度较高的地区,繁殖时,由温度高的地区迁回到温度较低的地区。迁徙时间一般在3月份前后和9月份前后,迁徙路线一般为沿海或沿江、沿湖地带。读图回答6~8题。
4.该功能区形成的主要原因是 ( )
A.城区中心,接近市场 B.临河濒海,环境优美
C.交通沿线,物流便捷 D.沿河分布,运费低廉
3.阴影区代表的功能区最有可能是 ( )
A.商业区 B.住宅区 C.工业区 D.仓储区
2.从可持续发展考虑,本区位于260米的地方最合理的土地利用方式是: ( )
A.种植水稻 B.种植小麦 C.种植柑橘 D.种植香蕉
读“我国某海滨小城功能区分布示意图”,完成3~5题。
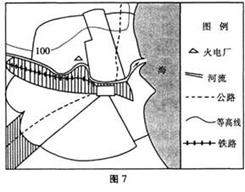
1.图示地区能见到的景观是: ( )
A.横看成岭侧成峰,远近高低各不同
B.椰林树荫,水清沙白
C.天苍苍,野茫茫,风吹草低见牛羊
D.山重水复疑无路,柳暗花明又一村
21.(本小题满分13分)
已知数列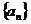 中,
中,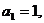 且点
且点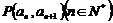 在直线{007}
在直线{007}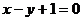 上。
上。
(1)求数列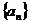 的通项公式;
的通项公式;
(2)若函数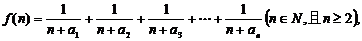 求函数
求函数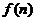 的最小值;
的最小值;
(3)设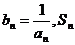 表示数列
表示数列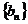 的前
的前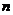 项和。试问:是否存在关于
项和。试问:是否存在关于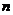 的整式
的整式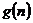 ,使得
,使得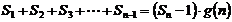 对于一切不小于2的自然数
对于一切不小于2的自然数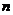 恒成立?
若存在,写出
恒成立?
若存在,写出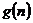 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
20.(本小题满分13分)
已知椭圆{007}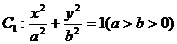 的离心率为
的离心率为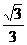 ,直线
,直线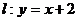 与以原点为圆心、椭圆
与以原点为圆心、椭圆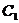 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。
(1)求椭圆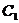 的方程;
的方程;
(2)设椭圆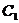 的左焦点为
的左焦点为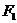 ,右焦点为
,右焦点为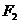 ,直线
,直线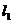 过点
过点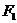 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线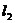 垂直于直线
垂直于直线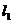 ,垂足为点
,垂足为点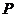 ,线段
,线段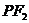 的垂直平分线交
的垂直平分线交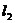 于点
于点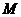 ,求点
,求点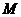 的轨迹
的轨迹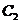 的方程;
的方程;
(3)设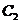 与
与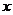 轴交于点
轴交于点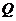 ,不同的两点
,不同的两点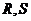 在
在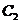 上,且满足
上,且满足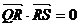 ,求
,求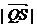 的取值范围。
的取值范围。
19.(本小题满分13分)
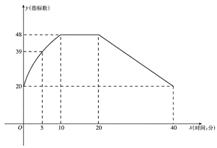
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散. 学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中). 当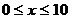 时,图象是抛物线的一部分,当
时,图象是抛物线的一部分,当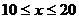 和
和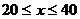 时,图象是线段.
时,图象是线段.
(1)当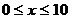 时,求注意力指标数y与时间x的函数关系式;
时,求注意力指标数y与时间x的函数关系式;
 (2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
18.(本小题满分12分)
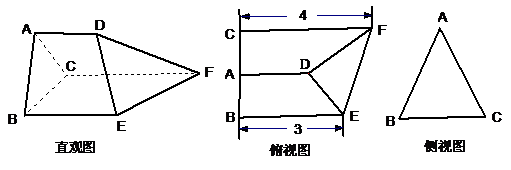
如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知 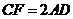 ,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.
,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.
(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角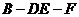 的余弦值.
的余弦值.
17.(本小题满分12分)
某篮球职业联赛的总决赛在甲队与乙队间角逐,采用五局三胜制,即若一队先胜三场,则此队获胜,比赛结束,因两队实力相当,每场比赛获胜的可能性相等,据以往资料统计,第一场比赛组织者可获门票收入30万元,以后每场比赛门票收入都比上一场增加10万元,问:
(1)组织者在此次总决赛中获得门票收入不少于180万元的概率是多少?
(2)用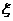 表示组织者在此次总决赛中的门票收入,求
表示组织者在此次总决赛中的门票收入,求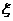 的数学期望?
的数学期望?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com