
7.在探究电路的电流规律实验时用了图8中的某个电路,已知R1=R2<R3,电流表的读数分
别是:A1为0.3A、A2为0.15A、A3为0.45A.测量时的电路图应是

[答案]B
[解析]A是串联电路,串联电路中电流:I=I1=I2(串联电路中各处的电流相等),不符合题意,A选项错误。
B,C,D都是并联电路,并联电路中①电流:I=I1+I2(干路电流等于各支路电流之和)
②电压:U=U1=U2(干路电压等于各支路电压)。B,C中A3的示数等于A1,A2之和,又由于R1=R2<R3 在C图中A1等于A2的示数,与题意不符。所以C错误,B正确。D选项中A2等于A1与A3的和,与题意不符,因此也是错误的。
[考点]串、并联电路特点
6.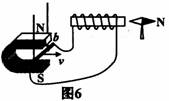 如图6所示,在蹄形磁体的磁场中放置一根与螺线管连
如图6所示,在蹄形磁体的磁场中放置一根与螺线管连
接的导体棒ab,当ab棒水平向右运动时,小磁针N极
转至右边.可使如图6所示位置的小磁针N极转至左边
的操作是图7中的
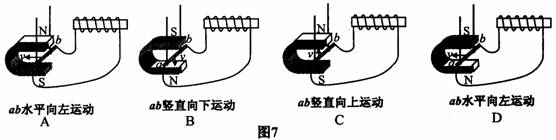
[答案]A
[解析]闭合电路的一部分导体在磁场中做切割磁感线运动,就会产生感应电流。感应电流的方向与磁场的方向和导体运动的方向有关。所以想改变感应电流的方向只要改变其中一个因素就行了。根据小磁针偏转方向可判定螺线管中的电流方向。由题意知需要小磁针想不通的方向偏转,只要改变感应电流方向就行了。
[考点]电磁感应
5. 图5中a、b是同一人的两幅照片,b图中他拿的眼镜
图5中a、b是同一人的两幅照片,b图中他拿的眼镜
A.属于凸透镜,可用于矫正近视眼
B.属于凸透镜,可用于矫正远视眼
C.属于凹透镜,可用于矫正远视眼
D.属于凹透镜,可用于矫正近视眼
[答案]B
[解析]由b图,我们看到他的眼睛的像的特点是正立放大的虚像,可知他拿的眼镜属于属于凸透镜,可用于矫正远视眼
[考点]凸透镜成像的特点及其应用
4.甲、乙两人同时从同一起跑线出发,同向做匀速直线运动,某时刻他们的位置如图3所
示,图4中能正确反映两人运动距离与时间关系的是( )

[答案]D
[解析]这是一道有关图形的,由图3可以看出相同的时间,乙跑的路程多。由于甲,乙做匀速直线运动,所以随着时间的增大,甲,乙行驶的路程也随着增大,A,B反映的随着时间的增加,路程不变,所以错误。C,D图中,可以从横坐标选择一点,做纵坐标的平行线,交甲乙与a,b两点,然后过a,b两点做横坐标的平行线,得到结论。
[考点]匀速直线运动
3.根据图2所给信息,判断下列说法正确的是
A.蝙蝠可以发出频率为400Hz的声音
B.人能听到蝙蝠发出的所有频率的声音
C.人听觉频率范围比人发声频率范围要大
D.15Hz的声音只要振幅足够大,人耳是能听到的
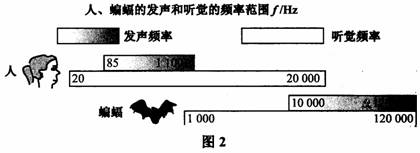
[答案]C
[解析]人听觉频率范围20Hz-20000 Hz,人发声频率范围85Hz-1100 Hz,C选项正确。蝙蝠的可以发出频率为10000 Hz,A选项错误。人的听觉频率也是有范围的,B选项错误。无论振幅多大,只要频率达不到人听觉频率范围,人耳是听不到声音的,D选项错误。
[考点]信息题,人耳的听觉频率范围
2.图1所示的电子体温计通过流过半导体制成的感温头的电流来反映人的体温,这利用了
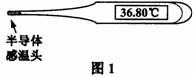 半导体
半导体
A.良好的导电特性
B.良好的绝缘特性
C.电阻随温度变化而变化的特性
D.电阻随光照变化而变化的特性
[答案]C
[解析]有的半导体受热后电阻随温度的升高而增大,利用这一特性可做成热敏电阻。电子体温计是利用感温元体(通常是用热敏电阻)的电阻值大小随环境温度的变化而变化的原理制成的。
[考点]半导体的特点
每小题给出的四个选项中,只有一项符合题意。
1.下列能源中属于可再生能源的是
A.风能 B.核能 C.石油 D.天然气
[答案]A
[解析]能源按照能否在短时间内得到补充和恢复,分为可再生能源和不可再生能源。核能、石油和天然气都是经过很长时间才形成的,消耗后无法在短时间内得到补充,属于不可再生能源,答案选A。
[考点]能源的分类
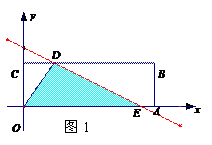
25.(2010广东广州,25,14分)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线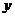 =-
=-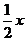 +
+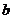 交折线OAB于点E.
交折线OAB于点E.
(1)记△ODE的面积为S,求S与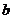 的函数关系式;
的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
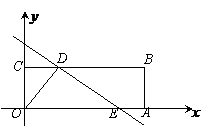

[分析](1)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;②如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积;
(2)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化.
[答案](1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=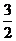
若直线经过点B(3,1)时,则b=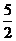
若直线经过点C(0,1)时,则b=1
①若直线与折线OAB的交点在OA上时,即1<b≤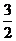 ,如图25-a,
,如图25-a,

此时E(2b,0)
∴S=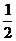 OE·CO=
OE·CO=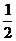 ×2b×1=b
×2b×1=b
②若直线与折线OAB的交点在BA上时,即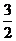 <b<
<b<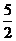 ,如图2
,如图2
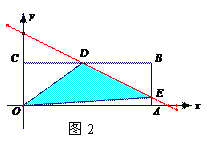

此时E(3,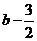 ),D(2b-2,1)
),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[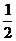 (2b-1)×1+
(2b-1)×1+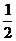 ×(5-2b)·(
×(5-2b)·(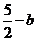 )+
)+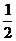 ×3(
×3(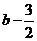 )]=
)]=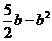
∴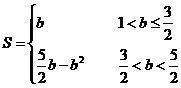
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
本题答案由无锡市天一实验学校金杨建老师草制!
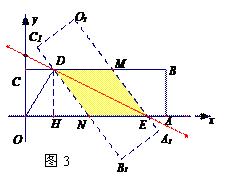

由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=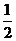 ,DH=1,∴HE=2,
,DH=1,∴HE=2,
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知: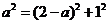 ,∴
,∴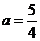
∴S四边形DNEM=NE·DH=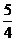
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为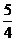 .
.
[涉及知识点]轴对称 四边形 勾股定理
[点评]本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.
[推荐指数]★★★★★
24.(2010广东广州,24,14分)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是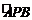 上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,若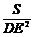 =4
=4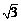 ,求△ABC的周长.
,求△ABC的周长.
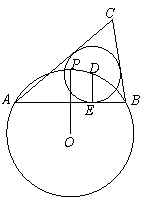

[分析](1)连接OA,OP与AB的交点为F,则△OAF为直角三角形,且OA=1,OF=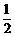 ,借助勾股定理可求得AF的长;
,借助勾股定理可求得AF的长;
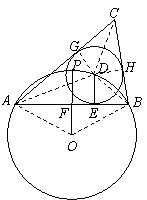

(2)要判断∠ACB是否为定值,只需判定∠CAB+∠ABC的值是否是定值,由于⊙D是△ABC的内切圆,所以AD和BD分别为∠CAB和∠ABC的角平分线,因此只要∠DAE+∠DBA是定值,那么CAB+∠ABC就是定值,而∠DAE+∠DBA等于弧AB所对的圆周角,这个值等于∠AOB值的一半;
(3)由题可知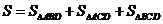 =
=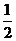 DE (AB+AC+BC),又因为
DE (AB+AC+BC),又因为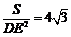 ,所以
,所以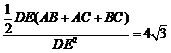 ,所以AB+AC+BC=
,所以AB+AC+BC=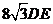 ,由于DH=DG=DE,所以在Rt△CDH中,CH=
,由于DH=DG=DE,所以在Rt△CDH中,CH=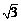 DH=
DH=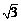 DE,同理可得CG=
DE,同理可得CG=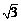 DE,又由于AG=AE,BE=BH,所以AB+AC+BC=CG+CH+AG+AB+BH=
DE,又由于AG=AE,BE=BH,所以AB+AC+BC=CG+CH+AG+AB+BH=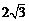 DE+
DE+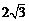 ,可得
,可得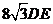 =
=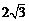 DE+
DE+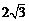 ,解得:DE=
,解得:DE=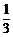 ,代入AB+AC+BC=
,代入AB+AC+BC=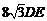 ,即可求得周长为
,即可求得周长为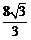 .
.
[答案]解:(1)连接OA,取OP与AB的交点为F,则有OA=1.


∵弦AB垂直平分线段OP,∴OF=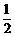 OP=
OP=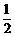 ,AF=BF.
,AF=BF.
在Rt△OAF中,∵AF=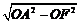 =
=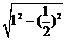 =
=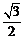 ,∴AB=2AF=
,∴AB=2AF=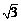 .
.
(2)∠ACB是定值.
理由:由(1)易知,∠AOB=120°,
因为点D为△ABC的内心,所以,连结AD、BD,则∠CAB=2∠DAE,∠CBA=2∠DBA,
因为∠DAE+∠DBA=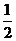 ∠AOB=60°,所以∠CAB+∠CBA=120°,所以∠ACB=60°;
∠AOB=60°,所以∠CAB+∠CBA=120°,所以∠ACB=60°;
(3)记△ABC的周长为l,取AC,BC与⊙D的切点分别为G,H,连接DG,DC,DH,则有DG=DH=DE,DG⊥AC,DH⊥BC.
∴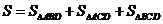
=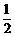 AB•DE+
AB•DE+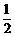 BC•DH+
BC•DH+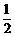 AC•DG=
AC•DG=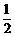 (AB+BC+AC) •DE=
(AB+BC+AC) •DE=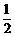 l•DE.
l•DE.
∵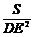 =4
=4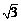 ,∴
,∴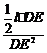 =4
=4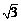 ,∴l=8
,∴l=8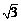 DE.
DE.
∵CG,CH是⊙D的切线,∴∠GCD=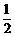 ∠ACB=30°,
∠ACB=30°,
∴在Rt△CGD中,CG=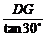 =
=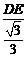 =
=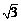 DE,∴CH=CG=
DE,∴CH=CG=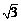 DE.
DE.
又由切线长定理可知AG=AE,BH=BE,
∴l=AB+BC+AC=2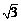 +2
+2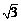 DE=8
DE=8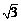 DE,解得DE=
DE,解得DE=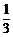 ,
,
∴△ABC的周长为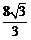 .
.
[涉及知识点]垂径定理 勾股定理 内切圆 切线长定理 三角形面积
[点评]本题巧妙将垂径定理、勾股定理、内切圆、切线长定理、三角形面积等知识综合在一起,需要考生从前往后按顺序解题,前面问题为后面问题的解决提供思路,是一道难度较大的综合题
[推荐指数]★★★★★
23.(2010广东广州,23,12分)已知反比例函数y=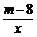 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图9,过点A作直线AC与函数y=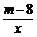 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
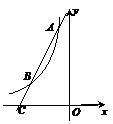

[分析](1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;(2)分别过点A、B作x轴的垂线,垂足分别为点D、E,则△CBE∽△CAD,运用相似三角形知识求出CE的长即可求出点C的横坐标.
[答案]解:(1)∵ 图像过点A(-1,6),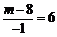 . ∴
. ∴
(2)分别过点A、B作x轴的垂线,垂足分别为点D、E,
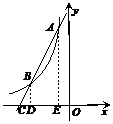

由题意得,AD=6,OD=1,易知,AD∥BE,
∴△CBE∽△CAD,∴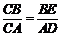 .
.
∵AB=2BC,∴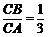
∴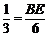 ,∴BE=2.
,∴BE=2.
即点B的纵坐标为2
当y=2时,x=-3,易知:直线AB为y=2x+8,
∴C(-4,0)
[涉及知识点]反比例函数
[点评]由于今年来各地中考题不断降低难度,中考考查知识点有向低年级平移的趋势,反比例函数出现在解答题中的频数越来约多.
[推荐指数]★★★★
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com