
2010.4
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分300分。考试时长150分钟。考生务必将答案写在答题卡和答题纸上,在试卷上作答无效。考试结束后,将本试卷、答题卡和答题纸一并交回。
以下数据可供解题时参考:
可能用到的相对原子质量:
H 1 C 12 N 14 O 16 Na 23 Cl 35.5 Fe 56 Cu 64 Zn 65
第I卷(选择题 共120分)
本卷共20小题。每题6分。共120分。在下列各题的四个选项中,只有一个选项是符合题目要求的。
7.已知函数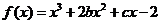 的图象在与
的图象在与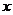 轴交点处的切线方程是
轴交点处的切线方程是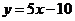 .
.
(I)求函数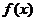 的解析式;
的解析式;
(II)设函数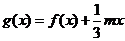 ,若
,若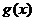 的极值存在,求实数
的极值存在,求实数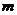 的取值范围以及函数
的取值范围以及函数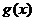 取得极值时对应的自变量
取得极值时对应的自变量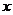 的值.
的值.
6.已知函数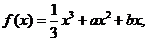 且
且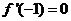
(I)试用含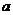 的代数式表示
的代数式表示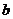 ;
;
(Ⅱ)求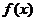 的单调区间;
的单调区间;
(Ⅲ)令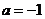 ,设函数
,设函数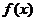 在
在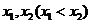 处取得极值,记点
处取得极值,记点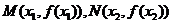 ,证明:线段
,证明:线段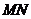 与曲线
与曲线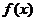 存在异于
存在异于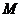 、
、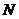 的公共点.
的公共点.
5.
已知函数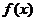 在R上满足
在R上满足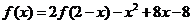 ,则曲线
,则曲线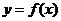 在点
在点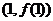 处的切线方程是
.
处的切线方程是
.
4. 定义在R上的函数f(x)满足f(x)= 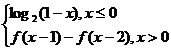 ,则f(2009)的值为
.
,则f(2009)的值为
.
3.已知定义在R上的奇函数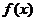 ,满足
,满足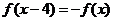 ,且在区间[0,2]上是增函数,则( )
,且在区间[0,2]上是增函数,则( )
A.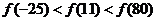 B.
B. 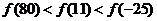
C.
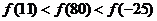 D.
D.
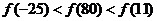
2.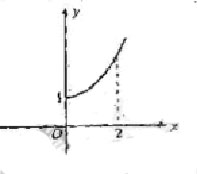 定义在R上的偶函数
定义在R上的偶函数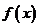 的部分图象如右图所示,则在
的部分图象如右图所示,则在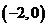 上,下列函数中与
上,下列函数中与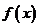 的单调性不同的是( )
的单调性不同的是( )
A.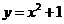 B.
B.
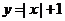
C. 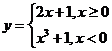 D.
D.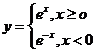
1.函数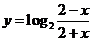 的图象( )
的图象( )
A.
关于原点对称
B.关于主线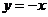 对称
对称
C.
关于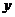 轴对称
D.关于直线
轴对称
D.关于直线 对称
对称
4.导数与单调性、极(最)值问题.
导数作为工具来研究三次函数、指数函数、对数函数的单调性,极值、最值时,具有其独特的优越性,要理解导数的几何意义,熟练导数的运算公式,善于借助导数解决有关的问题.
例4.已知函数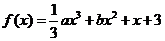 ,其中
,其中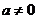 .
.
(1)当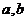 满足什么条件时,
满足什么条件时,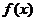 取得极值?
取得极值?
(2)已知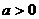 ,且
,且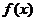 在区间
在区间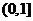 上单调递增,试用
上单调递增,试用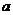 表示出
表示出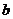 的取值范围.
的取值范围.
解析: (1)由已知得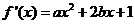 ,令
,令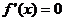 ,得
,得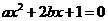 ,
,
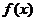 要取得极值,方程
要取得极值,方程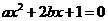 必须有解,
必须有解,
所以△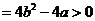 ,即
,即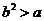 , 此时方程
, 此时方程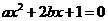 的根为:
的根为:
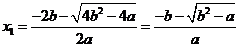 ,
,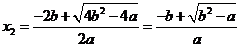 ,
,
所以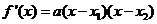 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
当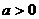 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以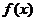 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当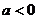 时,
时,
|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
F’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以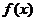 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当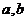 满足
满足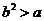 时,
时,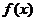 取得极值.
取得极值.
(2)要使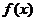 在区间
在区间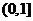 上单调递增,需使
上单调递增,需使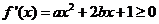 在
在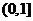 上恒成立.
上恒成立.
即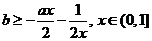 恒成立,所以
恒成立,所以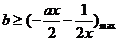 ,
,
设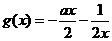 ,
,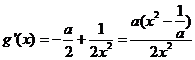 ,
,
令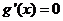 得
得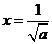 或
或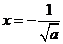 (舍去),
(舍去),
当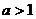 时,
时,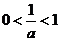 ,当
,当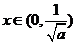 时
时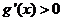 ,
,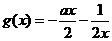 单调增函数;
单调增函数;
当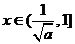 时
时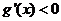 ,
,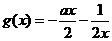 单调减函数,
单调减函数,
所以当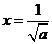 时,
时,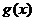 取得最大,最大值为
取得最大,最大值为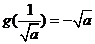 .
.
所以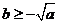 .
.
当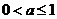 时,
时,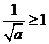 ,此时
,此时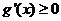 在区间
在区间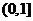 恒成立,
恒成立,
所以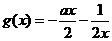 在区间
在区间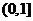 上单调递增,
上单调递增,
当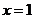 时
时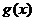 最大,最大值为
最大,最大值为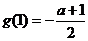 ,所以
,所以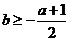 .
.
综上,当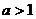 时,
时,
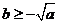 ;当
;当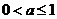 时,
时,
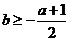 .
.
点评:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
[思想方法]
[例1]若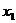 是方程
是方程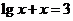 的解,
的解,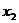 是
是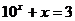 的解,则
的解,则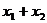 的值为( )
的值为( )
A. 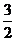 B.
B.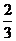 C.
C.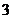 D.
D.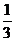
[解析]作出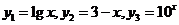 的图象,
的图象,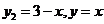 交点横坐标为
交点横坐标为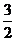 ,而
,而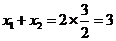 .
.
[答案]C
[点评]该题考查了指数函数、对数函数的图象及性质.综合了函数的图象、方程的解及曲线的交点等问题.指数函数、对数函数是两类重要的基本初等函数, 高考中以它们为载体的函数综合题既考查双基, 又考查对蕴含其中的函数思想、等价转化、分类讨论等思想方法的理解与运用.
[例2]若函数f(x)=a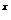 -x-a(a>0且a
-x-a(a>0且a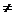 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 .
[解析]设函数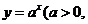 且
且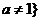 和函数
和函数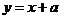 ,则函数f(x)=a
,则函数f(x)=a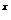 -x-a(a>0且a
-x-a(a>0且a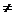 1)有两个零点,
就是函数
1)有两个零点,
就是函数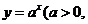 且
且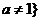 与函数
与函数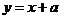 有两个交点,由图象可知当
有两个交点,由图象可知当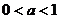 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当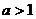 时,因为函数
时,因为函数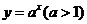 的图象过点(0,1),而直线
的图象过点(0,1),而直线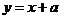 所过的点一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是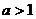 .
.
[答案]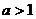
[点评]本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象解答.体现了对分类讨论思想的考查,分类讨论时,要注意该分类时才分类,讨论务必要全面.
[例3]已知偶函数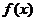 在区间
在区间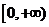 单调增加,则满足
单调增加,则满足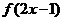 <
<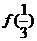 的x 取值范围是( )
的x 取值范围是( )
(A)(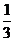 ,
,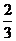 ) (B) [
) (B) [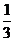 ,
,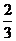 ) (C)(
) (C)(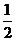 ,
,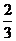 ) (D) [
) (D) [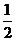 ,
,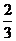 )
)
[解析]由于f(x)是偶函数,故f(x)=f(|x|),
∴得f(|2x-1|)<f(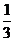 ),再根据f(x)的单调性,得|2x-1|<
),再根据f(x)的单调性,得|2x-1|<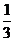 ,解得
,解得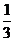 <x<
<x<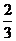 .
.
[答案]B
[点评]该题的关键是将含有函数符号的不等式转化为普通的不等式,体现的对转化思想的考查,同时还综合考查了函数的性质,而该题的转化的依据就是函数的奇偶性和单调性.考题中通过这种形式来考查函数的性质与方程、不等式等的综合不但是一个热点,而且成了一个固定的必考题型.
[专题演练]
3.函数的实际应用
函数的实际运用主要是指运用函数的知识、思想和方法综合解决问题.函数描述了自然界中量的依存关系,是对问题本身的数量本质特征和制约关系的一种刻画,用联系和变化的观点提出数学对象,抽象其数学特征,建立函数关系.掌握有关函数知识是运用函数思想的前提,考生应具备用初等数学思想方法研究函数的能力,运用函数思想解决有关数学问题的意识是运用函数思想的关键.
例3.某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x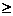 10)层,则每平方米的
平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
10)层,则每平方米的
平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
解析:设楼房每平方米的平均综合费为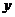 元,依题意得:
元,依题意得:
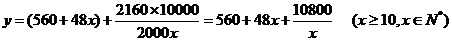 .
.
则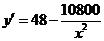 ,令
,令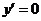 ,即
,即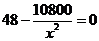 ,解得
,解得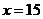 .
.
当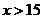 时,
时,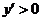 ;当
;当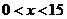 时,
时,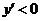 ,
,
因此,当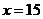 时,
时,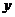 取得最小值,
取得最小值,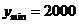 元.
元.
答:为了使楼房每平方米的平均综合费最少,该楼房应建为15层.
点评:这是一题应用题,利用函数与导数的知识来解决问题.利用导数,求函数的单调性、求函数值域或最值是一种常用的方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com