
3. “sin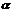 =
=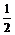 ”是“
”是“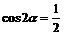 ”
” 的( )
的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
2.有四个关于三角函数的命题:
 :
: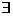 x
x R,
R, 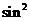
 +
+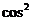
 =
=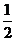 ;
; 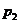 :
: 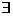 x、y
x、y R, sin(x-y)=sinx-siny;
R, sin(x-y)=sinx-siny;
 :
:  x
x
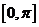 ,
,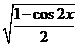 =sinx;
=sinx; 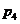 : sinx=cosy
: sinx=cosy x+y=
x+y=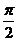 .
.
其中假命题的是( )
A. ,
,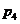 B.
B.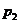 ,
,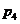 C.
C. ,
, D.
D.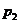 ,
,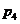
1.函数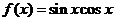 最小值是( )
最小值是( )
A.-1
B. 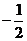 C.
C.
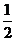 D.1
D.1
5.三角函数与简易逻辑的综合
高考对于简易逻辑的考查,总是与各部分知识综合在一起,达到考查基础知识的同时也考查简易逻辑的目的.而通过该类综合题考查三角函数部分的基本概念、性质和运算是历年来的热点.
例8.
“ ”是“
”是“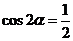 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:A
解析:当 时,
时,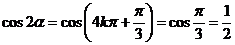 ,
,
反之,当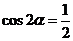 时,有
时,有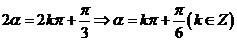 ,
,
或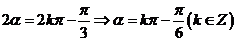 ,故应选A.
,故应选A.
点评:本题主要综合考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查.
[思想方法]
[例1]在同一平面直角坐标系中,函数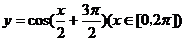 的图象和直线
的图象和直线 的交点个数是( )
的交点个数是( )
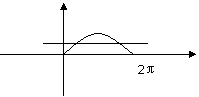 A.0 B.1
C.2
D.4
A.0 B.1
C.2
D.4
解析:原函数可化为:
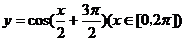 =
=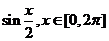 .
.
作出原函数图象,截取 部分,其与直线
部分,其与直线 的交点个数是2个.
的交点个数是2个.
[分析]该题是数形结合思想的体现,本小题主要考查三角函数图象的性质问题,学会五点法画图,取特殊角的三角函数值画图.掌握三角函数的周期等性质是准确作图的关键.
[例2]已知向量
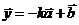 ,且
,且 ,
,
(1)求函数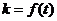 的表达式;
的表达式;
(2)若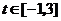 ,求
,求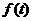 的最大值与最小值.
的最大值与最小值.
解析:(1) ,
,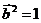 ,
,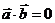 ,又
,又 ,
,
所以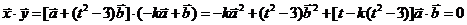 ,
,
所以 ,即
,即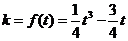 ;
;
(2)由(1)可得,令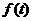 导数
导数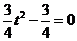 ,解得
,解得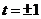 ,列表如下:
,列表如下:
|
t |
-1 |
(-1,1) |
1 |
(1,3) |
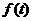 导数 导数 |
0 |
- |
0 |
+ |
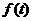 |
极大值 |
递减 |
极小值 |
递增 |
而 所以
所以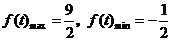 .
.
[分析]本题以三角函数和平面向量为载体,将三角函数与平面向量、导数等综合考察,体现了知识之间的融会贯通.考查了方程和函数思想,高考命题对思想方法的考查越来越得到重视.
[例3]已知函数 在区间
在区间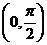 上单调递减,试求实数
上单调递减,试求实数 的取值范围.
的取值范围.
解析:任取
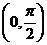 ,且
,且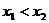 ,则不等式
,则不等式 恒成立,即:
恒成立,即:
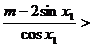
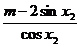 恒成立.化简得
恒成立.化简得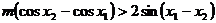 ,
,
由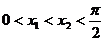 ,可知:
,可知: ,所以
,所以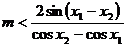 .
.
上式恒成立的条件为: 在区间
在区间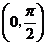 上的最小值.
上的最小值.
由于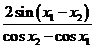
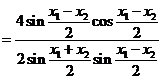
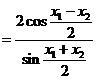
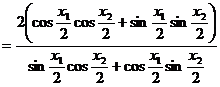
 .
.
且当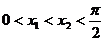 时,
时,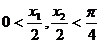 ,所以
,所以
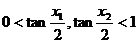 ,
,
从而

 ,
,
有 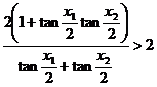 ,故
,故 的取值范围为
的取值范围为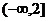 .
.
[分析]该题考查了转化与化归思想,根据已知条件,该题实际上是一个给出了在区间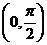 上恒成立的不等式.
上恒成立的不等式.
[专题演练]
4.三角函数与幂、指、对函数的综合
三角函数作为基本初等函数之一,具有函数的基本性质,如奇偶性、单调性、周期性,遵循复合函数图象的单调性规律,考题有时将三角函数与幂、指、对函数等结合构造复合函数研究其图象的性质也是命题的一个方向.
例7.函数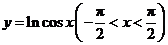 的图象是( )
的图象是( )


答案:A
解析: 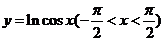 是偶函数,可排除B、D,由
是偶函数,可排除B、D,由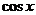 的值域可以确定.故选A.
的值域可以确定.故选A.
点评:本小题主要考查复合函数的图象识别,充分掌握偶函数的性质,余弦函数的图象及性质,另外,排除法,在复习时应引起重视,解选择题时,经常采用排除法.
3.解三角形的实际应用
对于正弦定理、余弦定理的综合考查,主要是以实际问题为载体,解决一些简单的三角形度量问题,和几何计算有关的问题.解三角形时,要灵活运用已知条件,根据正、余弦定理,列出方程,进而求解,最后还要检验是否符合题意.重点为正余弦定理及三角形面积公式,考题灵活多样,近几年经常以解答题的形式来考查,若以解决实际问题为背景的试题,有一定的难度.
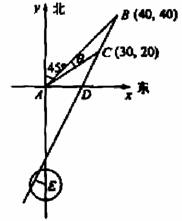 例6. 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东
例6. 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东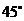 且与点A相距40
且与点A相距40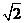 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东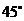 +
+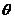 (其中sin
(其中sin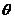 =
= ,
,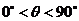 )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
解析: (I)如图,AB=40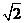 ,AC=10
,AC=10 ,
,
 .
.
由于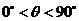 ,所以cos
,所以cos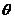 =
= .
.
由余弦定理得BC=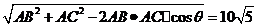 .
.
所以船的行驶速度为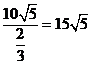 (海里/小时).
(海里/小时).
(II) 如图所示,以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1= 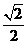 AB=40,x2=ACcos
AB=40,x2=ACcos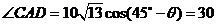 ,
,
y2=ACsin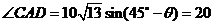 .
.
所以过点B、C的直线l的斜率k= ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=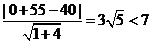 .
.
所以船会进入警戒水域.
点评:三角函数在实际问题中有很多的应用,随着课改的深入,联系实际,注重数学在实际问题的应用将分是一个热点.
2.三角函数与平面向量综合题
三角函数与平面向量是高中数学中两个活跃的“角色”,它们联手演绎了新颖度高,变化丰富的一幕幕好戏,三角函数与平面向量的综合性问题作为近年来的高考命题热点,难度不大,主要注重基础知识的考查,强调三角函数、平面向量的工具作用.从题型上看,主要包括向量与三角函数的化简、求值及证明的交汇,向量与三角函数图象、性质的交汇等.
 例4.将函数
例4.将函数 的图象按向量
的图象按向量 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( ).
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( ).
A. B.
B.
C.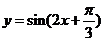 D.
D.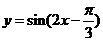
答案:C
解析:将函数 的图象按向量
的图象按向量 平移,即向左平移
平移,即向左平移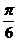 ,根据“左加右减”的平移规律,平移后的图象所对应的解析式为
,根据“左加右减”的平移规律,平移后的图象所对应的解析式为 ,由图象知,
,由图象知,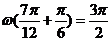 ,所以
,所以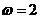 ,因此选C.
,因此选C.
点评:把按照向量平移转化为方向平移,再利用函数图象的平移规律“左加右减,上加下减”来解决问题.
例5. 已知向量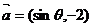 与
与 互相垂直,其中
互相垂直,其中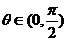 .
.
(1)求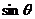 和
和 的值;
的值;
(2)若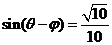 ,
, ,求
,求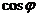 的值.
的值.
解析:(1)∵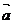 与
与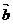 互相垂直,则
互相垂直,则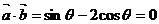 ,即
,即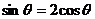 ,代入
,代入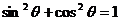 得
得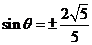 ,
,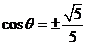 ,又
,又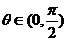 ,∴
,∴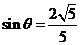 ,
,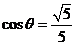 .
.
(2)∵ ,
,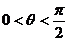 ,∴
,∴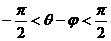 ,则
,则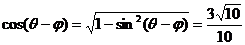 ,
,
∴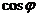
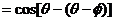
 .
.
点评:该题以向量为载体考查了三角函数的基本运算性质和向量的数量积.三角函数与平面向量的综合题在近几年的高考题中经常出现,难度不大,考题灵活多变,形式新颖,较好的考查了这两部分的基本知识和基本方法.
1. 三角函数图象与性质的综合
正、余弦函数在[0,2π],正切函数在(-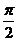 ,
,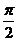 )的图象及性质,如单调性、最大值与最小值、有界性、对称性、周期性、图象与x轴的交点、函数图象平移的规律等一直是高考的重要内容.考查的形式通常是综合考查,以选择题、解答题为主,难度以容易题、中档题为主.
)的图象及性质,如单调性、最大值与最小值、有界性、对称性、周期性、图象与x轴的交点、函数图象平移的规律等一直是高考的重要内容.考查的形式通常是综合考查,以选择题、解答题为主,难度以容易题、中档题为主.
例1.将函数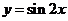 的图象向左平移
的图象向左平移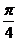 个单位, 再向上平移1个单位,所得图象的函数解析式是( )
个单位, 再向上平移1个单位,所得图象的函数解析式是( )
A.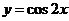 B.
B.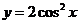 C.
C. D.
D.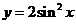
答案:B
解析:将函数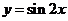 的图象向左平移
的图象向左平移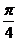 个单位,得到函数
个单位,得到函数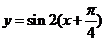 即
即 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为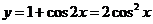 ,故选B.
,故选B.
点评:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,其中公式的变形在解决本题中起着很重要的作用.
例2.如果函数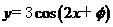 的图象关于点
的图象关于点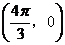 中心对称,那么
中心对称,那么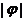 的最小值为( )
的最小值为( )
(A)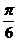 (B)
(B)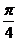 (C)
(C)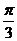 (D)
(D) 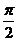
答案:C
解析:  函数
函数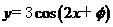 的图象关于点
的图象关于点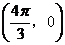 中心对称,
中心对称,
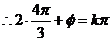
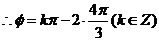 .由此易得
.由此易得 .故选C.
.故选C.
点评:该题考查了三角函数的图象和性质,对于三角函数图象的对称问题,要注意五点作图法中的五个基本点的坐标和整体思想的运用.
例3.已知函数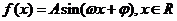 (其中
(其中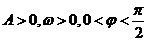 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为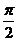 ,且图象上一个最低点为
,且图象上一个最低点为 .
.
(Ⅰ)求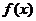 的解析式;
的解析式;
(Ⅱ)当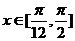 ,求
,求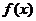 的值域.
的值域.
解析:(1)由最低点为 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为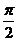 得
得 =
=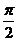 ,即
,即 ,
,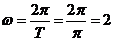 .
.
由点 在图象上的
在图象上的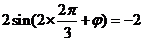 ,即
,即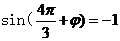 .
.
故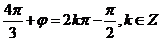
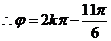 .
.
又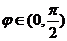 ,
, ,故
,故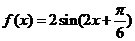 .
.
(2)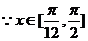 ,
,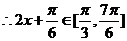
当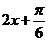 =
=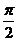 ,即
,即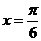 时,
时,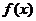 取得最大值2;
取得最大值2;
当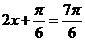 ,即
,即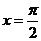 时,
时,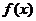 取得最小值-1,
取得最小值-1,
故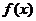 的值域为[-1,2].
的值域为[-1,2].
点评:该题综合考查了三角函数的图象和性质,对于三角函数图象的准确把握和对其性质的准确理解是解决该题必不可少的条件,求函数的值域时,一定要注意自变量的取值范围.
2.对该部分内容一般以选择、解答题的形式进行考查,且难度不大,主要考查以下四类问题:(1)与三角函数单调性有关的问题;(2)与三角函数图象有关的问题;(3)应用同角三角函数的基本关系和诱导公式求三角函数值及化简和等式证明的问题;(4)与周期有关的问题.
[知识交汇]
1.高考对该部分的考查主要是三角函数的图象与性质,对三角恒等变换的考查难度有所降低,解三角形是一个知识交汇点,将三角、向量、平面几何等知识综合起来考查.要求能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com