
20.(本题满分13分)
高新开发区某公司,生产一种品牌笔记本电脑的投入成本是4500/台。当笔记本电脑销售价为6000元/台时,月销售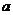 台;根据市场分析的结果表明,如果笔记本电脑的销售价提高的百分率为
台;根据市场分析的结果表明,如果笔记本电脑的销售价提高的百分率为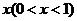 ,那么月销售量减少的百分率为
,那么月销售量减少的百分率为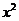 ,记销售价提高的百分率为
,记销售价提高的百分率为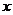 时,电脑企业的月利润是
时,电脑企业的月利润是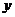 (元)。
(元)。
(1)写出月利润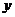 (元)与
(元)与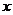 的函数关系式;
的函数关系式;
(2)如何确定这种笔记本电脑的销售价,使得该公司的月利润最大。
19.(本题满分12分)
已知,等差数列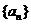 的首项
的首项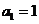 ,公差
,公差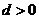 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列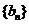 的第二项、第三项、第四项。
的第二项、第三项、第四项。
(1)求数列 的通项公式;
的通项公式;
(2)设数列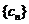 对任意正整数
对任意正整数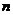 均有
均有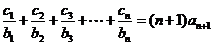 成立,求数列
成立,求数列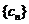 的前
的前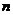 项的和
项的和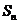
18.(本题满分12分)
如图,求直三棱柱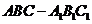 中,
中, ,点
,点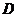 是
是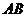 的中点。
的中点。
(1)求证: 平面
平面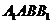 ;
;
(2)求证: 平面
平面
17.(本题满分12分)
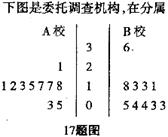 我市积极响应《全民健身条例》,大力开展学生体育活动,下图是委托调查机构,在分属两类不同性质的
我市积极响应《全民健身条例》,大力开展学生体育活动,下图是委托调查机构,在分属两类不同性质的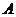 校和
校和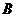 校中,随机抽取了10名高三年级学
校中,随机抽取了10名高三年级学
生,他们周体育锻炼时间的茎叶图(单位:10分钟)。
(1)根据茎叶图计算哪个学校学生总体活动时间多?
(2)如果从 校这10名学生中随机抽取体育锻炼时间
校这10名学生中随机抽取体育锻炼时间
不超过120分钟的两名同学,求至少抽到一名活动时间不足
1小时的同学的概率。
16.(本题满分12分)
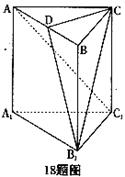
 如图,为了计算渭河岸边两景点
如图,为了计算渭河岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取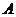 和
和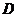 两个测量点,现测得
两个测量点,现测得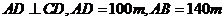 ,
,
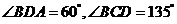 ,求两景点
,求两景点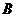 与
与 的距离(假设
的距离(假设
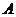 ,
,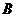 ,
, ,
,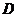 在同一平面内,测量结果保留整数;参考数据:
在同一平面内,测量结果保留整数;参考数据:
 。)
。)
15.(这里给出3道选做题,考生只能从中选做一题,多答时,按序只评第1题。)
(几何证明选讲做题)如图所示,圆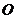 的直径
的直径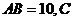 为圆周上一点,
为圆周上一点,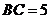 ,过
,过 作圆的切线
作圆的切线 ,则点A到直线
,则点A到直线 的距离
的距离 为__________;
为__________;
(坐标系与参数方程选讲做题)直线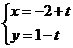 (
( 为参数)被圆
为参数)被圆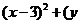
 =25所截得的弦长为__________。
=25所截得的弦长为__________。
(不等式选讲选做题)若不等式 对一切非零实数
对一切非零实数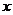 均成立,则实数
均成立,则实数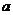 的最大值是__________。
的最大值是__________。
14.在实数的原有运算中,我们补充定义新运算“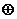 ”如下:当
”如下:当 时,
时, ;当
;当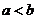 时,
时, ,设函数
,设函数 ,则函数
,则函数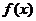 的值域为___________。
的值域为___________。
13.已知函数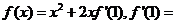 _____________。
_____________。
12.某算法流程图如图所示,则输出结果是_________。
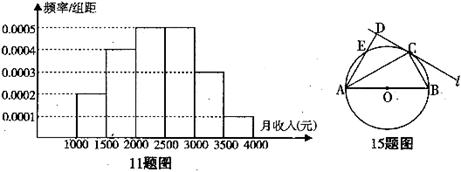
11. 市统计调查队就市区居民的月收入调查了10000人,并根据所得数据绘制了样本的频率分布直方图(如右图),为了分析居民的收入与年龄、学历、职业等方面的关系,要从这1000人中再用分层抽样方法抽出100人作进一步调查,则在
市统计调查队就市区居民的月收入调查了10000人,并根据所得数据绘制了样本的频率分布直方图(如右图),为了分析居民的收入与年龄、学历、职业等方面的关系,要从这1000人中再用分层抽样方法抽出100人作进一步调查,则在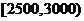 (元)的月收入段应抽出__________人。
(元)的月收入段应抽出__________人。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com