
20.( 本小题满分14分)已知函数
(1)当m=1时,求函数f(x)的最小值;
(2)若函数 存在两个零点,求m的取值范围
存在两个零点,求m的取值范围
(3)证明: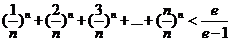
19.(本小题满分13分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
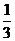 |
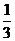 |
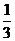 |
概率 |
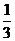 |
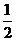 |
 |
(1)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(2)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(3)若两个射手各射击1次,记所得的环数之和为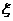 ,求
,求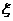 的分布列和期望。
的分布列和期望。
18.(本小题满分13分)
甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系 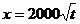 。若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格)。
。若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格)。
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额y=0.002t2(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?
17.(本小题满分13分)
如图,已知四棱锥 的底面是直角梯形,∠ABC
的底面是直角梯形,∠ABC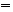 ∠BCD
∠BCD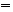 90°,AB
90°,AB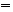 BC
BC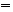 PB
PB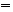 PC
PC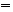 2CD
2CD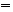 2,侧面PBC⊥底面ABCD。
2,侧面PBC⊥底面ABCD。
(1)求证: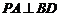 ;
;
(2)求二面角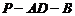 的余弦值。
的余弦值。
16.(本小题满分13分)
设数列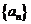 的前
的前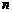 项和为
项和为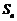 ,且满足
,且满足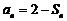
 .
.
(1)求 ,
,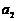 ,
, ,
,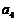 的值并猜想这个数列的通项公式
的值并猜想这个数列的通项公式
(2)证明数列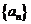 是等比数列.
是等比数列.
15.对于实数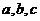 ,若在⑴
,若在⑴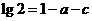
⑵
⑶ ⑷
⑷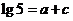
⑸ 中
中
有且只有两个式子是不成立的,则不成立的式子是
14.若三角形内切圆半径为 ,三边长分别
,三边长分别
为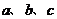 ,则三角形的面积
,则三角形的面积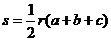 ,
,
根据类比思想,若四面体内切球半径为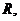 其四
其四
个面的面积分别为 ,则四面体
,则四面体
的体积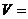 ____________________
____________________
13.如果执行右边的程序框图,则输出的
S= 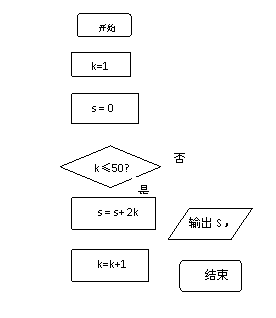
12.已知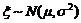 ,且
,且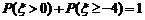 ,则
,则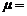 _________。
_________。
11.若 则在展开式各项系数中最大值等于
;
则在展开式各项系数中最大值等于
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com