
1.Where are the two speakers?
A.In a restaurant. B.In a
hotel. C.In th e street.
e street.
21.(本题满分13 分)
已知函数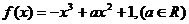
(1)若在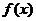 的图象上横坐标为
的图象上横坐标为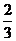 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若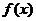 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数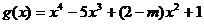 的图象与函数
的图象与函数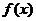 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
19.(本小题满分13 分)
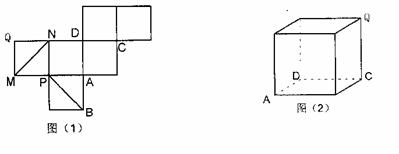
如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
(1)求证:MN//平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P-DB-M 的大小.
|
已知椭圆的右焦点F 与抛物线y2 = 4x 的焦点重合,短轴长为2.椭圆的右准线l与x轴交于E,过右焦点F 的直线与椭圆相交于A、B 两点,点C 在右准线l 上,BC//x 轴.
(1)求椭圆的标准方程,并指出其离心率;
(2)求证:线段EF被直线AC 平分.
18.(本小题满分12 分)
已知{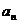 }是整数组成的数列,a1 = 1,且点
}是整数组成的数列,a1 = 1,且点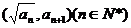 在函数
在函数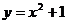 的图象上,
的图象上,
(1)求数列{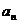 }的通项公式;
}的通项公式;
(2)若数列{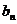 }满足
}满足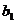 = 1,
= 1,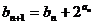 ,求证:
,求证: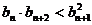
17.(本小题满分12 分)
从甲地到乙地一天共有A、B 两班车,由于雨雪天气的影响,一段时间内A 班车正点到达乙地的概率为0.7,B 班车正点到达乙地的概率为0.75。
(1)有三位游客分别乘坐三天的A 班车,从甲地到乙地,求其中恰有两名游客正点到达的概率(答案用数字表示)。
(2)有两位游客分别乘坐A、B 班车,从甲地到乙地,求其中至少有1 人正点到达的概率(答案用数字表示)。
16. (本小题满分12 分)
(本小题满分12 分)
已知函数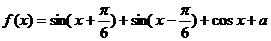 的最大值为1.
的最大值为1.
(1)求常数a 的值;
(2)求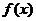 的单调递增区间;
的单调递增区间;
(3)求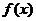 ≥ 0 成立的x 的取值集合.
≥ 0 成立的x 的取值集合.
15.对正整数n,设曲线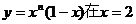 处的切线与y轴交点的纵坐标为
处的切线与y轴交点的纵坐标为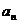 ,
,
(i)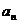 =
=
(ii)数列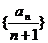 的前n项和Sn=
的前n项和Sn=
14.设向量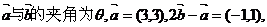 若直线
若直线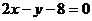 沿向量
沿向量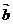 平移,所得直线过双曲线
平移,所得直线过双曲线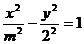 的右焦点,
的右焦点,
(i)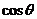 =
=
(ii)双曲线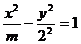
 的离
心率e=
.
的离
心率e=
.
13.已知函数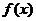 是R 上的偶函数,且在(0,+
是R 上的偶函数,且在(0,+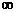 )上有
)上有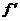 (x)> 0,若f(-1)= 0,那么关于x的不等式x f(x)< 0 的解集是____________.
(x)> 0,若f(-1)= 0,那么关于x的不等式x f(x)< 0 的解集是____________.
12.设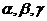 是三个不重合的平面,l 是直线,给出下列四个命题:
是三个不重合的平面,l 是直线,给出下列四个命题:
①若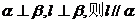 ;
;
②若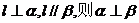 ;
;
③若l上有两点到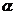 的距离相等,则l//
的距离相等,则l//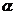 ;
;
④若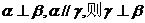 .
.
其中正确命题的序号是____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com