
18.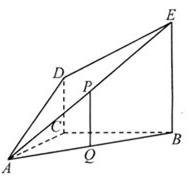 (本小题满分12分) 如图,
(本小题满分12分) 如图,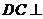 平面
平面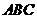 ,
,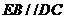 ,
,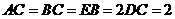 ,
,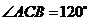 ,
,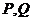 分别为
分别为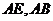 的中点.
的中点.
(1)证明: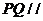 平面
平面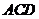 ;
;
(2)求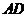 与平面
与平面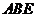 所成角的正弦值.
所成角的正弦值.
[解析](1)证明:连接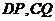 , 在
, 在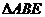 中,
中,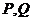 分别是
分别是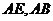 的中点,所以
的中点,所以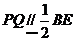 , 又
, 又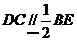 ,所以
,所以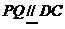 ,又
,又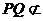 平面ACD ,DC
平面ACD ,DC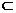 平面ACD,
所以
平面ACD,
所以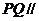 平面ACD
平面ACD
(2)在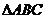 中,
中,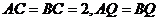 ,所以
,所以
而DC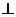 平面ABC,
平面ABC,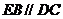 ,所以
,所以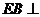 平面ABC
平面ABC
而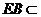 平面ABE,
所以平面ABE
平面ABE,
所以平面ABE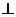 平面ABC,
所以
平面ABC,
所以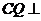 平面ABE
平面ABE
由(1)知四边形DCQP是平行四边形,所以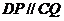
所以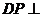 平面ABE,
所以直线AD在平面ABE内的射影是AP,
平面ABE,
所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是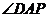
在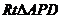 中,
中,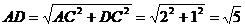 ,
,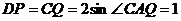
所以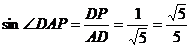
17.(本小题满分12分)
已知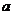 从
从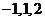 中任取一个数,
中任取一个数,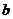 从
从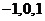 中任取一个数.
中任取一个数.
(1)求函数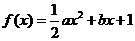 有零点的概率;
有零点的概率;
(2)求使两个不同向量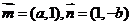 的夹角
的夹角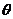 为锐角的概率.
为锐角的概率.
[解析]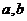 的取值共有9种(
的取值共有9种(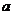 的值在前,
的值在前,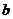 的值在后):
的值在后):

(1)记“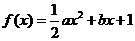 有零点”为事件A,∵
有零点”为事件A,∵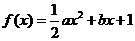 有零点,
有零点,
即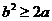 ,满足条件的
,满足条件的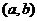 有3个:
有3个: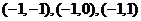 .
. 概率
概率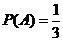 .
.
(2)记“两个不同向量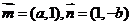 的夹角
的夹角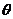 为锐角”为事件B,
为锐角”为事件B,
由条件有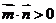 且
且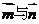 不共线,所以
不共线,所以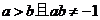 .符合条件的
.符合条件的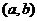 有4个:
有4个: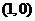 ,
,
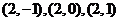 .
.  概率
概率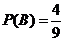 .
.
16.(本小题满分12分) 在锐角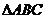 中,已知内角
中,已知内角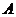 、
、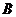 、
、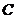 的对边分别为
的对边分别为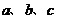 .向量
.向量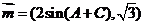 ,
,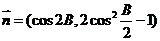 ,且向量
,且向量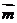 、
、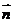 共线.
共线.
(1) 求角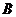 的大小;
的大小;
(2) 如果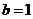 ,求
,求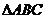 面积的最大值.
面积的最大值.
[解析](1)∵向量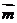 、
、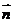 共线,∴
共线,∴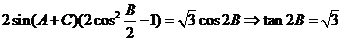 ,
,
∵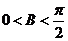 ,∴
,∴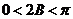 ,∴
,∴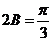 ,
,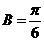 .
.
(2)由余弦定理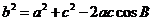 ,即
,即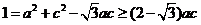 ,所以
,所以 ,
,
(当且仅当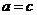 时取等号)
时取等号)
所以 ,故
,故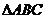 面积的最大值为
面积的最大值为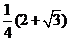 .
.
15.在区间[0,1]上任取两个实数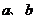 ,则函数
,则函数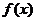 =
=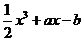 在区间[-1,1]上有且只有
在区间[-1,1]上有且只有
一个零点的概率为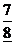 .
.
[解析]∵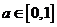 ,∴
,∴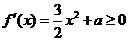 在[-1,1]恒成立,即
在[-1,1]恒成立,即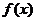 在[-1,1]为单调递增函数,
在[-1,1]为单调递增函数,
又函数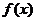 在区间[-1,1]上有且只有一个零点,所以
在区间[-1,1]上有且只有一个零点,所以 ,得概率为
,得概率为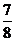 .
.
14.在极坐标系中,点 的距离为_______.
的距离为_______.
[解析]点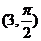 的直角坐标是
的直角坐标是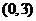 ,直线
,直线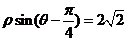 的直角坐标方程是
的直角坐标方程是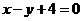 ,
,
由点到直线距离公式得所求距离为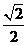 .
.
13.一个几何体的三视图如图所示:其中,主视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为 .

[解析]由三视图知该几何体是底面边长为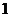 ,高为
,高为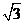 的正六棱锥,体积
的正六棱锥,体积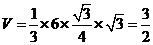
12.某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过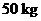 按
按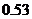 元/
元/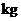 收费,超过
收费,超过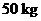 的部分按
的部分按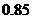 元/
元/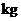 收费.相应收费系统的流程
收费.相应收费系统的流程
图如右图所示,则①处应填________________________.
[解析]因为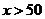 ,所以
,所以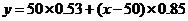
11.已知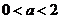 ,复数
,复数 的实部为
的实部为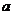 ,虚部为1,则
,虚部为1,则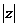 的取
的取
值范围是_____________.
[解析]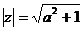 ,而
,而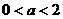 ,即
,即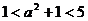 ,
,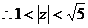
10. 已知非零向量
已知非零向量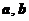 满足:
满足: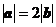 ,且
,且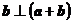 ,则向量
,则向量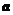 与向量
与向量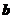 的夹角
的夹角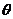 =
.
=
.
[解析] ,
, ,
,
9.抛物线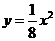 的焦点坐标是__________.
的焦点坐标是__________.
[解析]抛物线的标准方程是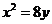 ,
,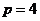 ,所以焦点坐标为
,所以焦点坐标为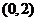
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com