
3.设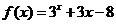 ,用二分法求方程
,用二分法求方程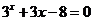 在
在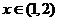 内近似解的过程中得
内近似解的过程中得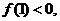
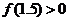 ,
,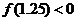 ,则方程的根落在区间
,则方程的根落在区间
A.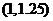 B.
B. C.
C.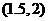 D.不能确定
D.不能确定
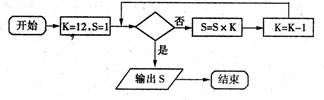
2.程序框图如图:如果上述运行的结果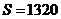 ,那么判断框中应填入
,那么判断框中应填入
A.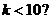 B.
B. C.
C.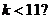 D.
D.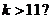
1. 集合
集合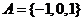 ,
,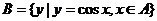 ,则
,则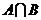 =
=
A.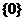 B.
B.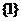
C. D.
D.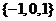
(17)解:由题意,得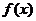 =
=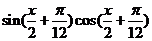 -
-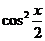 =
=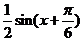 -
- =
=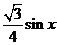 -
-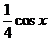 -
-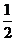 =
=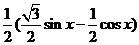 -
-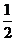 =
= -
-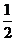 .
.
⑴∵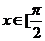 ,
,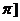 ,
,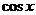 =-
=-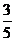 ,∴
,∴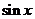 =
=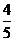 ,
,
∴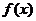 =
=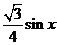 -
-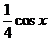 -
-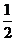 =
=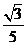 -
-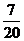 .
.
⑵由图象变换得,平移后的函数为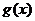 =
=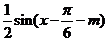 +n-
+n-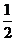 ,而平移后的图象关于原点对称,所以有:
,而平移后的图象关于原点对称,所以有: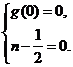
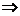
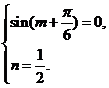
当注意到0<m<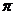 时,得
时,得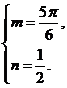
即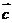 = (
= (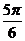 ,
,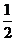 ).
).
(18)(理科做)解: (Ⅰ)“一次取出的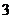 个小球上的数字互不相同”的事件记为
个小球上的数字互不相同”的事件记为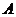 ,
,
则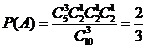 .
.
(Ⅱ)由题意得,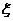 有可能的取值为:
有可能的取值为: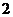 ,
,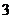 ,
,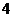 ,
,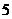 .
.
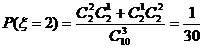 ,
,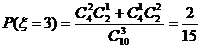
|
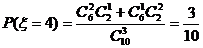 ,
,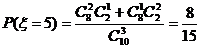
所以随机变量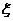 的概率分布为
的概率分布为
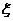
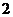
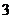
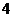
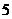
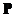
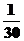
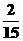
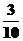

因此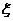 的数学期望为:
的数学期望为:
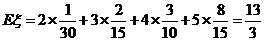 .
.
(文科做)记“甲从第一个口袋中的10个球中任意取出1个球是白球”记为事件A,“乙从第二个口袋中的10个球中任意取出1个球是白球”为事件B,……1分
于是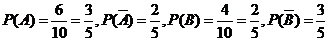 ,……5分
,……5分
由于甲或乙是否取得白球对对方是否取到白球没有影响,
因此,A与B是相互独立事件,……7分
(1)两人都取到白球的概率为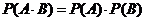 =
=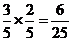 ;……9分
;……9分
(2)甲、乙两人均未取到白球的概率为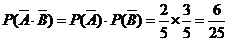 ,……10分
,……10分
则两人中至少有一人取到白球的概率为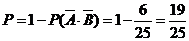 .……12分
.……12分
(19)解析:(理)(法一)(1)取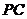 的中点
的中点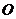 ,连结
,连结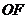 、
、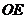 ,
,
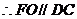 ,且
,且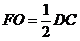 ,
,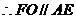 ,……2分
,……2分
又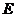 是
是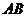 的中点,且
的中点,且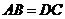 ,
,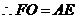 ,
,
∴四边形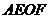 是平行四边形,∴
是平行四边形,∴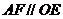 ,
,
又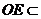 平面
平面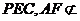 平面
平面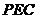 ,
,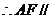 平面
平面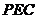 ;……4分
;……4分
(2)连结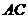 ,
,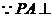 平面
平面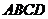 ,
,
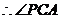 是直线
是直线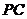 与平面
与平面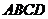 所成的角,……6分
所成的角,……6分
在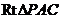 中,
中,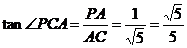 ,
,
即直线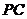 与平面
与平面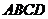 所成的角大小为
所成的角大小为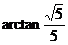 ;……8分
;……8分
(3)作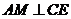 ,交
,交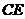 的延长线于
的延长线于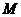 ,连结
,连结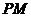 ,
,
由三垂线定理,得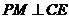 ,
,
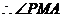 是二面角
是二面角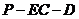 的平面角,……10分
的平面角,……10分
由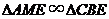 ,可得
,可得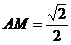 ,
,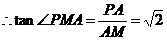 ,
,
∴二面角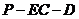 的大小为
的大小为 .……12分
.……12分
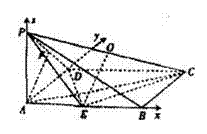
(法二)以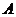 为原点,如图建立直角坐标系,则
为原点,如图建立直角坐标系,则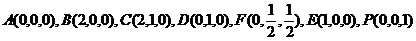 ,
,
(1)取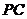 的中点
的中点 ,连结
,连结 ,
,
则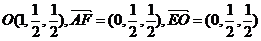 ,
, ,……2分
,……2分
又 平面
平面 平面
平面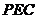 ,
,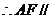 平面
平面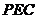 ;……4分
;……4分
(2)由题意可得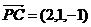 ,平面
,平面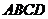 的法向量
的法向量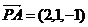 ,
,
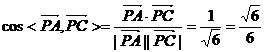 ,……6分
,……6分
即直线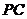 与平面
与平面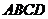 所成角的大小为
所成角的大小为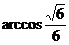 ;…………8分
;…………8分
(3)设平面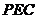 的法向量为
的法向量为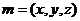 ,
,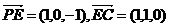 ,
,
则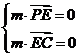 ,可得
,可得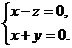
令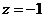 ,则m=(-1,1,-1),……10分
,则m=(-1,1,-1),……10分
由(2)可得平面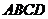 的法向量是
的法向量是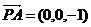 ,
,
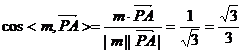 ,
,
∴二面角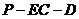 的大小为
的大小为 .……12分
.……12分
(文)(1)连接BD1,已知E、F分别为DD1、DB的中点,EF是三角形BD1D的中位线,∴EF//BD1,……2分
又EF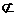 面BD1C1,BD1
面BD1C1,BD1 面BD1C1,∴EF//面BD1C1;……4分
面BD1C1,∴EF//面BD1C1;……4分
(2)连接BD1、BC1,
正方体中,D1C1^面BCC1B1,BC1Ì面BCC1B1,
所以D1C1^B1C,
在正方形BCCB中,两对角线互相垂直,即BC1^B1C,……6分
D1C1、BC1Ì面BC1D1,所以B1C^面BC1D1,
BD1Ì面BC1D1,所以有B1C^BD1,
在(1)已证EF//BD1,所以EF^B1C;……8分
(3)由三垂线定理知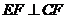 ,又∵
,又∵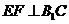 ,∴
,∴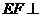 面
面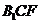 ,由三垂线定理知
,由三垂线定理知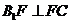 ,
,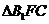 为直角三角形,
为直角三角形,
计算得:EB1=3,EF=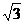 ,FB1=
,FB1=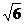 ,FC=
,FC= ,B1C=2
,B1C=2 ,…10分
,…10分
∴V=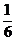 B1F·FC·EF=
B1F·FC·EF=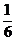 ×
× ×
×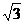 ×
×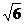 =1.……12分
=1.……12分
(20)(Ⅰ)依题意得 a=2c,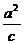 =4,解得a=2,c=1,从而b=
=4,解得a=2,c=1,从而b=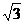 .故椭圆的方程为
.故椭圆的方程为 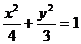 .
.
(Ⅱ)由(Ⅰ)得A(-2,0),B(2,0).设M(x0,y0).
 ∵M点在椭圆上,∴y0=
∵M点在椭圆上,∴y0=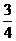 (4-x02).
①
(4-x02).
①
又点M异于顶点A、B,∴-2<x0<2,由P、A、M三点共线可以得P(4,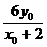 ).
).
从而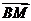 =(x0-2,y0),
=(x0-2,y0),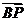 =(2,
=(2,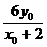 ).
).
∴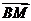 ·
·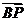 =2x0-4+
=2x0-4+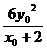 =
=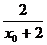 (x02-4+3y02).
②
(x02-4+3y02).
②
将①代入②,化简得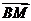 ·
·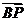 =
= (2-x0).
(2-x0).
∵2-x0>0,∴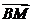 ·
·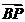 >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内.
(21)解:⑴∵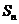 =
=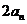 -2,∴当n≥2时,
-2,∴当n≥2时,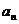 =
=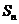 -
-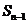 =
=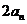 -
-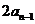 ,
,
即n≥2时,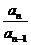 =2,数列
=2,数列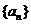 为等比数列.
为等比数列.
∵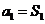 ,∴
,∴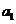 =
=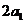 -2,即
-2,即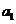 = 2,∴
= 2,∴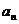 =
=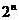 .
.
∵点P( ,
,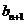 )在直线x-y+2 = 0上,
)在直线x-y+2 = 0上,
∴ -
-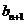 +2 = 0,即
+2 = 0,即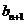 -
- = 2,所以数列
= 2,所以数列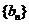 为等差数列,
为等差数列,
又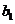 = 1,可得
= 1,可得 = 2n-1.
= 2n-1.
⑵由已知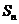 =
=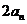 -2 =
-2 =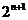 -2,
-2,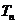 =
=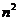 .
.
即证明不等式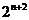 >
>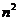 +3n+4,(n≥2,n
+3n+4,(n≥2,n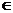 N*)
N*)
下面用数学归纳法证明如下:
①当n = 2时,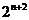 = 16,
= 16,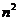 +3n+4 = 14,不等式成立;
+3n+4 = 14,不等式成立;
②假设当n = k (k≥2)时,原不等式成立,即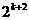 >
>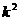 +3k+4成立,
+3k+4成立,
那么当n = k+1时,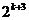 =
=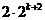 >2(
>2(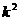 +3k+4) =
+3k+4) =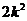 +6k+8,
+6k+8,
∵k≥2,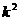 +k>0,即
+k>0,即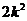 +6k+8 = (
+6k+8 = (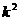 +k)+(
+k)+(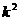 +5k+8)>
+5k+8)>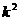 +5k+8 =
+5k+8 = +3(k+1)+4,
+3(k+1)+4,
∴当n = k+1时,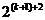 >
> +3(k+1)+4成立,
+3(k+1)+4成立,
综合①②可得原不等式成立.
(22)解:⑴函数 的定义域为(-1 ,+∞).
∵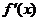 = 2[(x+1)-
= 2[(x+1)-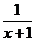 ] =
] =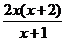 ,由
,由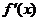 >0得x>0,由
>0得x>0,由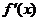 <0得-1<x<0,
<0得-1<x<0,
∴函数的递增区间是(0 ,+∞),递减区间是(-1 ,0).
⑵由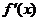 =
=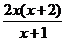 = 0得x = 0,由⑴知
= 0得x = 0,由⑴知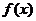
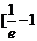 ,
,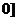 上单调递减,在[0,
上单调递减,在[0,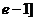 上单调递增.
上单调递增.
又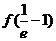 =
=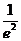 +2,
+2,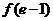 =
=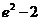 ,且
,且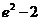 >
>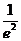 +2,所以当
+2,所以当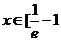 ,
,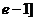 时,函数
时,函数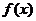 的最大值为
的最大值为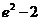 ,故当m>
,故当m>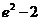 时,不等式
时,不等式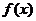 <m成立;
<m成立;
⑶由方程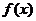 =
=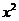 +x+a
+x+a x-a+1-
x-a+1-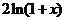 = 0,
= 0,
记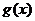 = x-a+1-
= x-a+1-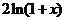 ,则
,则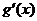 =1-
=1-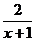 =
=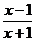 ,
,
由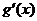 >0,得x>1,由
>0,得x>1,由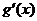 <0,得-1<x<1,所以
<0,得-1<x<1,所以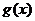 在[0,1]上递减,在[1,2]上递增.
在[0,1]上递减,在[1,2]上递增.
为使程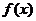 =
=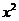 +x+a在区间[0,2]上恰好有两个相异的实根,只须
+x+a在区间[0,2]上恰好有两个相异的实根,只须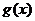 = 0在[0,1]和(1,2
= 0在[0,1]和(1,2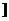 上各有一个实根,于是有
上各有一个实根,于是有
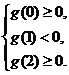
 2-
2-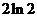 <a≤3-
<a≤3-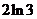 .
.
(13)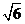 解析:由
解析:由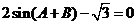 可得:
可得: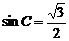 ,由
,由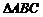 是锐角三角形,可知
是锐角三角形,可知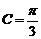 .由韦达定理:
.由韦达定理: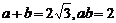 ,
,
因此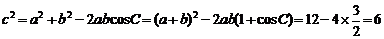 ,故
,故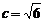 .
.
(14)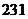 解:分三类,第一类,分给3个人,每人至少一个球;将20个球排成一排,一共有19个空隙,将两个隔板插入这些空隙中,规定由隔板分成的左、中、右三部分球分别分给3个人,则每一种隔法对应了一种分法,每一种分法对应了一种隔法,于是,此类的不同分法的总数为
解:分三类,第一类,分给3个人,每人至少一个球;将20个球排成一排,一共有19个空隙,将两个隔板插入这些空隙中,规定由隔板分成的左、中、右三部分球分别分给3个人,则每一种隔法对应了一种分法,每一种分法对应了一种隔法,于是,此类的不同分法的总数为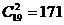 种方法;第二类,分给3个人中的两人;将20个球排成一排,一共有19个空隙,将1个隔板插入这些空隙中,这样就将20个球分成了两份,再将两份分给三人中的两个人,于是,
种方法;第二类,分给3个人中的两人;将20个球排成一排,一共有19个空隙,将1个隔板插入这些空隙中,这样就将20个球分成了两份,再将两份分给三人中的两个人,于是,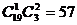 种方法;第三类,分给一个人,共3种方法;于是,共有不同的分法为
种方法;第三类,分给一个人,共3种方法;于是,共有不同的分法为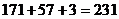 种;
种;
(15)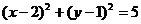 提示:由题意知此平面区域表示的是以
提示:由题意知此平面区域表示的是以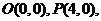
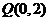 构成的三角形及其内部,且△
构成的三角形及其内部,且△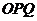 是直角三角形,如图, 所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是
是直角三角形,如图, 所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是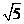 , 所以圆
, 所以圆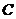 的方程是
的方程是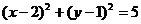 .
.
(16) 解:由题意知,长方体的对角线即为其外接球的直径,故2R =
解:由题意知,长方体的对角线即为其外接球的直径,故2R =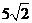
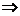 R =
R =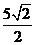 ,因此所求表面积为:
,因此所求表面积为: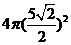 =
=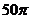 .
.
(1) (理)A;提示:根据题意可得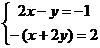 ,解得
,解得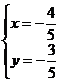 ,即
,即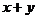 =
= ;
;
(文科做)A;提示:直接利用两角和的正弦公式;
(2)B
(3)C 解: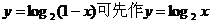 关于y轴的对称图形,可得
关于y轴的对称图形,可得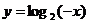 的图象,再向右平移一个单位,即可得
的图象,再向右平移一个单位,即可得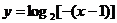 的图象,即
的图象,即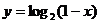 的图
的图
|
(4)C 解: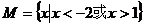
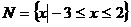 ,可以求出
,可以求出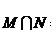
 .选C.
.选C.
(5)D;提示:共有身高符合国庆阅兵标准的士兵45人,抽取容量为9的样本,抽样比为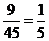 ,故抽取年龄在26岁-29岁的士兵人数为
,故抽取年龄在26岁-29岁的士兵人数为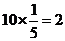 ,故选D.
,故选D.
(6)C解:设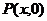 ,则
,则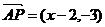 ,
,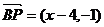 ,
,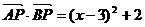 ,
,
显然,当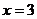 时,
时,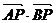 取得最小值
取得最小值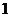 ;此时,
;此时,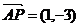 ,
,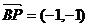 ,那么
,那么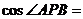
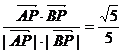
(7)B;提示:由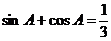 ,可得
,可得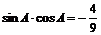 ,又
,又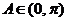 ,∴
,∴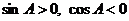 ,则
,则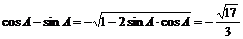 ,∴
,∴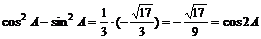 ;
;
(8)B解:由于点B到焦点的距离等于点B到准线的距离,又由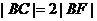 ,可得直线
,可得直线 的倾斜角为
的倾斜角为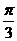 ;由
;由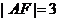 ,可得点A的纵坐标为
,可得点A的纵坐标为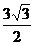 ,而点A的横坐标为
,而点A的横坐标为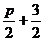
于是,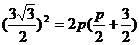 ,从而得,
,从而得,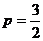 ;
;
(9)C解:设直径被分成的两部分分别为r、3r,由题意,(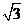 )
)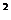 = r·3r,解得r = 1,则球
= r·3r,解得r = 1,则球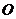 的半径R = 2,故
的半径R = 2,故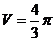 ·R
·R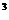 =
=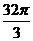 ,故选C.
,故选C.
(10)B解:由题意知,P在右支上,所以|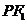 |-|
|-|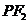 | = 2a,即|
| = 2a,即|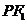 | =|
| =|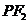 |+2a,
|+2a,
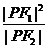 =
=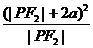 = 4a+|
= 4a+|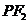 |+
|+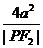 ≥4a+
≥4a+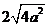 ,当且仅当|
,当且仅当|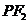 | =
| =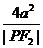 ,即|
,即|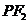 | = 2a时,等号成立,
| = 2a时,等号成立,
又|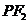 |≥c-a,2a≥c-a,解得
|≥c-a,2a≥c-a,解得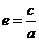 ≤3,故选B.
≤3,故选B.
(11)B 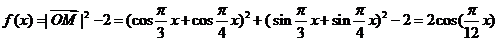 .
.
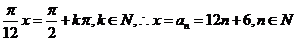 ,所以
,所以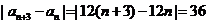 .
.
 (12)D解:圆方程化为(x+
(12)D解:圆方程化为(x+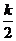 )
)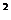 +(y
+(y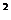 +
+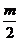 )
)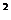 = 4+
= 4+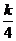
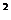 +
+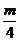
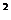 ,圆心为(-
,圆心为(-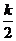 ,-
,-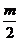 ),因为M、N关于直线x+y-1 = 0对称,所以直线x+y-1 = 0过圆心(-
),因为M、N关于直线x+y-1 = 0对称,所以直线x+y-1 = 0过圆心(-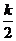 ,-
,-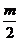 ),则-
),则-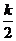 -
-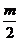 -1= 0,即k+m+2 = 0,又由题意知直线y =
kx+1与直线x+y-1 = 0垂直,所以k = 1,把k = 1代入k+m+2 = 0得m =-3,所以不等式组为:
-1= 0,即k+m+2 = 0,又由题意知直线y =
kx+1与直线x+y-1 = 0垂直,所以k = 1,把k = 1代入k+m+2 = 0得m =-3,所以不等式组为: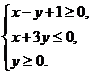 如图,阴影部分的面积为
如图,阴影部分的面积为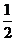 ×1×
×1×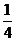 =
= ,故选D.
,故选D.
(17)(本题满分10分)已知向量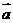 = (
= (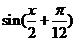 ,
,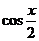 ),
),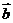 = (
= (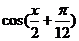 ,-
,-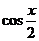 ),
),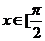 ,
,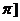 ,函数
,函数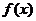 =
=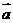 ·
·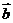 .⑴若
.⑴若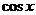 =-
=-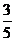 ,求函数
,求函数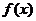 的值;
的值;
⑵将函数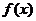 的图象按向量
的图象按向量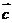 = (m,n) (0<m<
= (m,n) (0<m<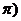 平移,使得平移后的图象关于原点对称,求向量
平移,使得平移后的图象关于原点对称,求向量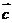 .
.
(18)(理科做)(本题满分12分)袋中装着标有数字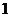 ,
,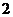 ,
,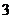 ,
,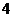 ,
,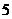 的小球各
的小球各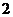 个,从袋中任取
个,从袋中任取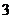 个小球,每个小球被取出的可能性都相等,用
个小球,每个小球被取出的可能性都相等,用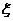 表示取出的
表示取出的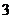 个小球上的最大数字,求:
个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量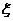 的概率分布和数学期望.
的概率分布和数学期望.
(文科做)有两个口袋,其中第一个口袋有6个白球,4个红球,第二个口袋中有4个白球,6个红球,甲从第一个口袋中的10个球中任意取出1个球 ,乙从第二个口袋中 的10个球任意取出一个球.
(1)求两人都取到白球的概率;
(2)求两人中至少有一个取到白球的概率.
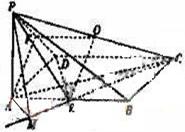
(19)(本题满分12分)(理科做)已知在四棱锥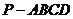 中,底面
中,底面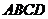 是矩形,
是矩形,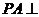 平面
平面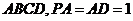 ,
,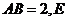 、
、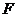 分别是
分别是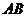 、
、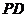 的中点,
的中点,
(1)求证: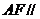 平面
平面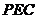 ;
;
(2)求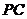 与平面
与平面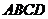 所成角的大小;
所成角的大小;
(3)求二面角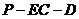 的大小.
的大小.
(文科做)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(1)求证:EF//平面BC1D1;
(2)求证:EF⊥B1C;
(3)求三棱锥B1-EFC的体积.

(20)(本题满分12分)设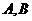 分别为椭圆
分别为椭圆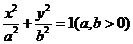 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且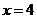 为它的右准线.
为它的右准线.
(Ⅰ)求椭圆的方程;
(Ⅱ)设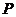 为右准线上不同于点(4,0)的任意一点, 若直线
为右准线上不同于点(4,0)的任意一点, 若直线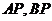 分别与椭圆相交于异于
分别与椭圆相交于异于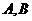 的点
的点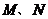 ,证明:点
,证明:点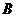 在以
在以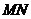 为直径的圆内.
为直径的圆内.
(21)(本题满分12分)已知数列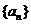 的前n项和为
的前n项和为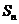 ,且
,且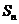 =
=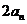 -2 (n = 1、2、3、…),数列
-2 (n = 1、2、3、…),数列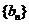 中,
中,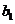 = 1,点P(
= 1,点P( ,
,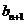 )在直线x-y+2 = 0上.
)在直线x-y+2 = 0上.
⑴求数列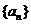 和数列
和数列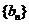 的通项公式;
的通项公式;
⑵若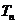 为数列
为数列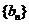 的前n项和,求证:当n≥2,n
的前n项和,求证:当n≥2,n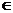 N*时,
N*时,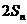 >
>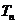 +3n.
+3n.
(22)(本题满分12分)设函数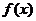 =
=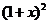 -
-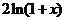 .
.
⑴求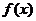 的单调区间;
的单调区间;
⑵若当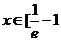 ,
,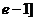 时(其中
时(其中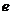 =2.718…)不等式
=2.718…)不等式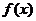 <m恒成立,求实数m的取值范围;
<m恒成立,求实数m的取值范围;
⑶若关于x的方程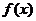 =
=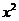 +x+a在区间[0,2]上恰好有两个相异的实根,求实数a的取值范围.
+x+a在区间[0,2]上恰好有两个相异的实根,求实数a的取值范围.
鄢陵县第一高中2010届第3次模拟考试试卷
(13)锐角三角形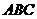 中,边长
中,边长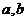 是方程
是方程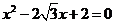 的两个根,且
的两个根,且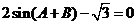 ,则
,则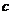 边的长是
.
边的长是
.
(14)20个相同的球分给3个人,允许有人可以不取,但必须分完,则不同的分法总数为 ;(用数字作答)
(15)已知平面区域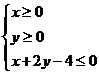 恰好被面积最小的圆
恰好被面积最小的圆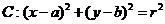 及其内部所覆盖,则圆
及其内部所覆盖,则圆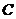 的方程为
.
的方程为
.
(16)长方体的对角线长度是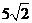 ,若长方体的8个顶点在同一球面上,则这个球的表面积是_____________.
,若长方体的8个顶点在同一球面上,则这个球的表面积是_____________.
(1)(理科做)若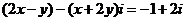 (
(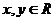 ),则
),则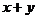 等于( )
等于( )
A.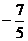 B.
B. C.
C.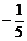 D.
D.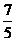
(文科做)sin(α-β)cos(β-γ)+cos(α-β)sin(β-γ)=( )
(2)若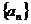 为等差数列,且有
为等差数列,且有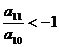 ,它的前
,它的前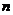 项和
项和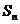 有最大值,那么当
有最大值,那么当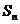 取得最小正值时,
取得最小正值时,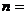 ( )
( )
A.1 B.19 C.17 D.18
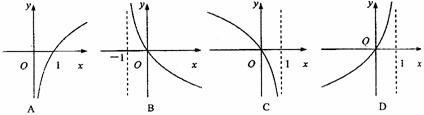
(3)函数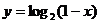 的图象是( )
的图象是( )
(4)已知集合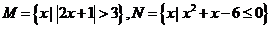 ,则
,则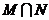 等于( )
等于( )
A.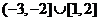 B.
B.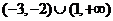
C.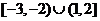 D.
D.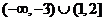
(5)某连队身高符合建国60周年国庆阅兵标准的士兵共有45人,其中18岁-21岁的士兵有15人,22岁-25岁的士兵有20人,26岁-29岁的士兵有10人,若该连队有9个参加国庆阅兵的名额,如果按年龄分层选派士兵,那么,该连队年龄在26岁-29岁的士兵参加国庆阅兵的人数为 ( )
A.5 B.4 C.3 D.2
(6)已知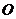 为坐标原点,
为坐标原点,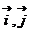 分别表示与
分别表示与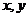 轴方向一致的单位向量,若
轴方向一致的单位向量,若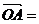
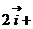
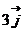 ,
,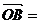
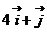 ,在
,在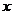 轴上有一点
轴上有一点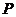 ,若
,若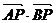 最小,则
最小,则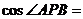 ( )
( )
A.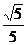 B.
B.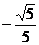
 C.
C.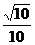 D.
D.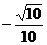
(7)已知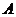 是三角形的一内角,且
是三角形的一内角,且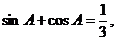 则
则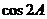 等于( )
等于( )
A.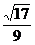 B.
B.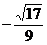 C.
C.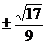 D.
D.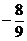
(8)如图,过抛物线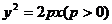 的焦点
的焦点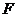 的直线
的直线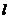 交抛
交抛
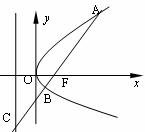 物线于点A、B,交其准线于点C,若
物线于点A、B,交其准线于点C,若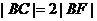 ,且
,且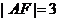 ,
,
则此抛物线的方程为 ( )
A.
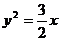 B
B
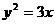
C.
 D.
D.
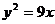
(9)球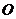 的截面把垂直于截面的直径分为1∶3两部分,若截面圆半径为
的截面把垂直于截面的直径分为1∶3两部分,若截面圆半径为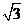 ,则球
,则球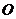 的体积为( ).
的体积为( ).
A.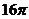 B.
B.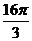 C.
C.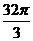 D.
D.
(10)已知双曲线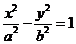 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为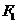 、
、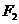 ,P为双曲线右支上任意一点,当
,P为双曲线右支上任意一点,当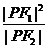 取得最小值时,该双曲线离心率的最大值为( ) .
取得最小值时,该双曲线离心率的最大值为( ) .
A.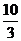 B.3
C.
B.3
C. D.2
D.2
(11)设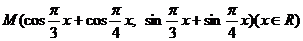 为坐标平面上一点,记
为坐标平面上一点,记 ,且
,且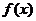 的图像与射线
的图像与射线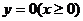 交点的横坐标由小到大依次组成数列
交点的横坐标由小到大依次组成数列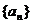 ,则
,则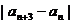 =( )
=( )
A.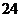 B.
B.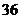 C.
C.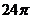 D.
D.
(12)如果直线y = kx+1与圆x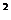 +y
+y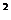 +kx+my-4 = 0交于M、N两点,且M、N关于直线x+y-1 = 0对称,则不等式组:
+kx+my-4 = 0交于M、N两点,且M、N关于直线x+y-1 = 0对称,则不等式组: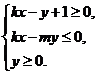 表示平面区域的面积是( ).
表示平面区域的面积是( ).
A.1
B.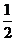 C.
C.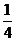 D.
D.
第二卷(非选择题部分,共90分)
21.A [解析]本题考查楞次定律及感应电流大小判断问题,难度中等。
线框刚进入磁场时磁通量向外增加,感应磁场向里,因此感应电流方向为顺时针,选项BD错误;随着线框的运动,导线切割磁感线长度增加,感应电流增加,A正确,C错误。本题正确选项为A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com