
7、对于抛物线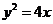 上任意一点
上任意一点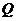 ,点
,点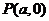 都满足
都满足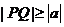 ,则
,则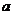 的取值范围是 ( )
的取值范围是 ( )
(A) 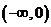 (B)
(B) 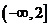 (C)
(C) 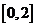 (D)
(D) 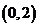
6、若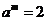 ,
,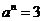 ,
,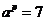
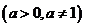 ,用m,n,p表示
,用m,n,p表示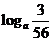 为( )
为( )
(A) 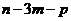 (B)
(B) 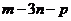 (C)
(C) 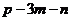 (D)
(D) 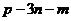
5、若函数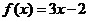 ,则
,则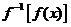 等于 ( )
等于 ( )
(A) 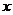 (B)
(B) 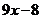 (C)
(C) 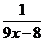 (D)
(D) 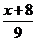
4、双曲线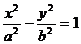 的一个焦点为F1,顶点为A1、A2,P是双曲线上任意一点.则分别以线段PF1、A1A2为直径的两圆一定 ( )
的一个焦点为F1,顶点为A1、A2,P是双曲线上任意一点.则分别以线段PF1、A1A2为直径的两圆一定 ( )
(A)相交 (B)相切 (C)相离 (D)以上情况均有可能
3、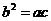 是“
是“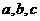 成等比数列”的 ( )
成等比数列”的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D) 既不充分又不必要条件
2、实数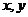 适合方程
适合方程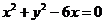 ,则
,则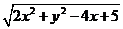 的值域是 ( )
的值域是 ( )
(A) 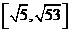 (B)
(B) 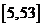 (C)
(C) 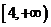 (D)
(D)
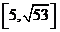
1、在数列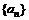 和
和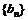 中,
中,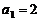 ,且对于任意自然数
,且对于任意自然数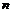 ,
,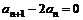 ,
,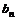 是
是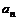 与
与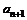 的等差中项,则
的等差中项,则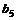 等于 ( )
等于 ( )
(A) 96 (B) 48 (C) 32 (D) 24
12.已知函数f(x)的定义域为R,且满足f(x+2)=-f(x).
(1)求证:f(x)是周期函数;
(2)若f(x)为奇函数,且当0≤x≤1时,f(x)=x,求使f(x)=-在[0,2010]上的所有x的个数.
解:(1)证明:∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),
∴f(x)是以4为周期的周期函数.
(2)当0≤x≤1时,f(x)=x,
设-1≤x≤0,则0≤-x≤1,∴f(-x)=(-x)=-x.∵f(x)是奇函数,∴f(-x)=-f(x),∴-f(x)=-x,即f(x)=x.故f(x)=x(-1≤x≤1)
又设1<x<3,则-1<x-2<1,∴f(x-2)=(x-2),
又∵f(x-2)=-f(2-x)=-f[(-x)+2]=-[-f(-x)]=-f(x),∴-f(x)=(x-2),∴f(x)=-(x-2)(1<x<3).∴f(x)=
由f(x)=-,解得x=-1.∵f(x)是以4为周期的周期函数.故f(x)=-的所有x=4n-1(n∈Z).令0≤4n-1≤2010,则≤n≤502,又∵n∈Z,∴1≤n≤502(n∈Z),∴在[0,2010]上共有502个x使f(x)=-.
11.已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).(1)求证:f(x)是奇函数;(2)如果x∈R+,f(x)<0,并且f(1)=-,试求f(x)在区间[-2,6]上的最值.
解:(1)证明:∴函数定义域为R,其定义域关于原点对称.
∵f(x+y)=f(x)+f(y),令y=-x,∴f(0)=f(x)+f(-x).令x=y=0,∴f(0)=f(0)+f(0),得f(0)=0.∴f(x)+f(-x)=0,得f(-x)=-f(x),∴f(x)为奇函数.
(2)法一:设x,y∈R+,∵f(x+y)=f(x)+f(y),∴f(x+y)-f(x)=f(y).
∵x∈R+,f(x)<0,∴f(x+y)-f(x)<0,∴f(x+y)<f(x).∵x+y>x,∴f(x)在(0,+∞)上是减函数.又∵f(x)为奇函数,f(0)=0,∴f(x)在(-∞,+∞)上是减函数.∴f(-2)为最大值,f(6)为最小值.∵f(1)=-,∴f(-2)=-f(2)=-2f(1)=1,f(6)=2f(3)=2[f(1)+f(2)]=-3.∴所求f(x)在区间[-2,6]上的最大值为1,最小值为-3.
法二:设x1<x2,且x1,x2∈R.则f(x2-x1)=f[x2+(-x1)]=f(x2)+f(-x1)=f(x2)-f(x1).∵x2-x1>0,∴f(x2-x1)<0.∴f(x2)-f(x1)<0.即f(x)在R上单调递减.∴f(-2)为最大值,f(6)为最小值.∵f(1)=-,∴f(-2)=-f(2)=-2f(1)=1,f(6)=2f(3)=2[f(1)+f(2)]=-3.∴所求f(x)在区间[-2,6]上的最大值为1,最小值为-3.
10.已知f(x)是R上的奇函数,且当x∈(-∞,0)时,f(x)=-xlg(2-x),求f(x)的解析式.
解:∵f(x)是奇函数,可得f(0)=-f(0),∴f(0)=0.当x>0时,-x<0,由已知f(-x)=xlg(2+x),∴-f(x)=xlg(2+x),即f(x)=-xlg(2+x) (x>0).
∴f(x)=即f(x)=-xlg(2+|x|)(x∈R).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com