
10. 11. _ 12.
7. 8. 9.
4. 5. 6.
共70分,把答案填在下面的横线上.)
1. 2. 3.
20.(本题满分16分)
设函数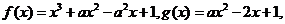 其中实数
其中实数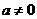 .
.
(1)当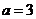 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当函数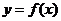 与
与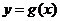 的图象只有一个公共点且
的图象只有一个公共点且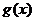 存在最小值时,
存在最小值时,
记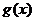 的最小值为
的最小值为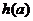 ,求函数
,求函数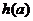 的值域;
的值域;
(3)若函数 与
与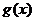 在区间
在区间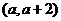 内均为增函数,求实数
内均为增函数,求实数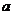 的取值范围.
的取值范围.
 2009-2010学年度第二学期期末考试
2009-2010学年度第二学期期末考试
高二数学答题纸(文科) 得分


19.(本题满分16分)
某地区有100户农民,都从事水产养殖。据了解,平均每户的年收入为3万元。为了调整产业结构,当地政府决定动员部分农民从事水产加工。据估计,如果能动员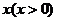 户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高
户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高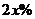 ,而从事水产加工的农民平均每户的年收入将为
,而从事水产加工的农民平均每户的年收入将为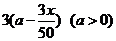 万元.
万元.
(1)在动员 户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求
户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求 的取值范围;
的取值范围;
(2)若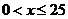 ,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求
,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求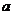 的最大值.
的最大值.
18.(本题满分16分)
已知函数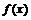 是定义在
是定义在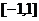 上的奇函数
,当
上的奇函数
,当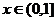 时,
时,
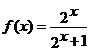
(1)判断函数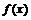 在区间
在区间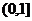 上的单调性,并用单调性的定义证明;
上的单调性,并用单调性的定义证明;
(2)求函数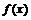 在
在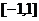 上的解析式;
上的解析式;
(3)求函数 的值域.
的值域.
17.(本题满分14分)
若函数 =
=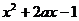 的图象过点
的图象过点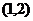
(1)求函数 的解析式
;
的解析式
;
(2)求函数 在区间
在区间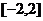 上的最小值和最大值.
上的最小值和最大值.
16.(本题满分14分)
已知复数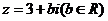 ,且
,且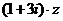 为纯虚数.
为纯虚数.
(1)求复数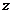 ;
;
(2)若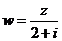 ,求复数
,求复数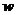 的模
的模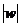 .
.
15.(本题满分14分)
设全集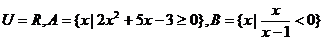
求(1)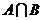 (2)CU(
(2)CU(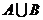 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com