
8.平面直角坐标系有点
(1)求向量 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);
(2)求θ的最值.
解:(1)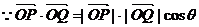
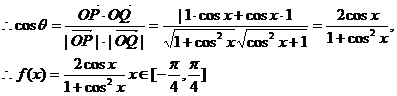
(2)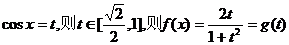
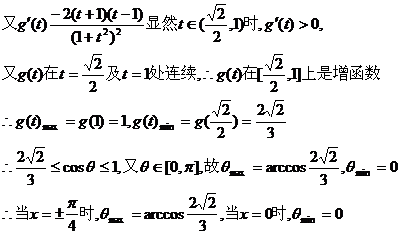
7.已知二次函数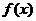 对任意
对任意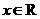 ,都有
,都有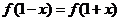 成立,设向量
成立,设向量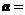 (sinx,2),
(sinx,2),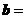 (2sinx,
(2sinx,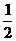 ),
),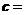 (cos2x,1),
(cos2x,1),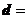 (1,2),当
(1,2),当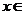 [0,
[0,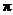 ]时,求不等式f(
]时,求不等式f(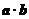 )>f(
)>f(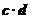 )的解集.
)的解集.
解析:设f(x)的二次项系数为m,其图象上两点为(1-x,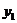 )、B(1+x,
)、B(1+x,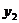 )因为
)因为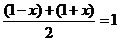 ,
,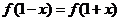 ,所以
,所以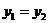 ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵ 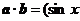 ,
,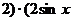 ,
,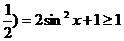 ,
,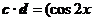 ,
,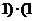 ,
,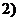
 ,
,
∴ 当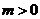 时,
时,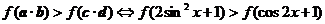
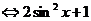
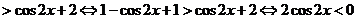
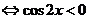
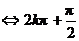
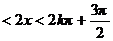 ,
,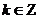 .
.
∵ 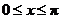 , ∴
, ∴ 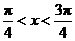 .
.
当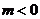 时,同理可得
时,同理可得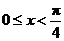 或
或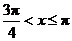 .
.
综上: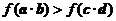 的解集是当
的解集是当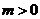 时,为
时,为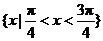 ;
;
当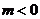 时,为
时,为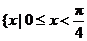 ,或
,或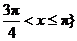 .
.
6.已知函数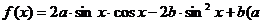 、b为常数,且
、b为常数,且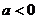 )的图象过点(
)的图象过点(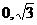 ),且函数
),且函数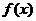 的最大值为2.
的最大值为2.
(1)求函数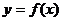 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
(2)若函数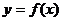 的图象按向量
的图象按向量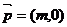 作移动距离最小的平移后,使所得的图象关于y轴对称,求出向量
作移动距离最小的平移后,使所得的图象关于y轴对称,求出向量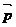 的坐标及平移后的图象对应的函数解析式
的坐标及平移后的图象对应的函数解析式
解:(1)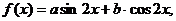
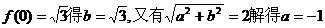
所以函数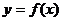 的解析式是
的解析式是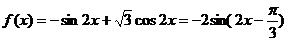
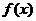 的单调递增区间是
的单调递增区间是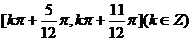
(2)∵平移后的图象对应的函数解析式是
图象关于y轴对称,即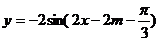 为偶函数,
为偶函数,
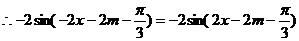
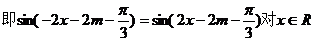 恒成立
恒成立
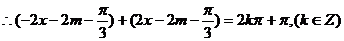
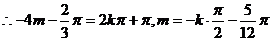 ,
,
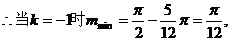
故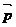
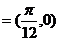 ,图象对应的函数解析式为
,图象对应的函数解析式为
5.设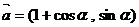 ,
,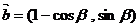 ,
,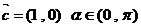
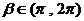 ,
,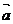 与
与 的夹角为
的夹角为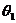 ,
,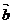 与
与 的夹角为
的夹角为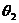 ,且
,且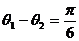 ,求
,求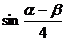 的值.(本题12分)
的值.(本题12分)
.解:
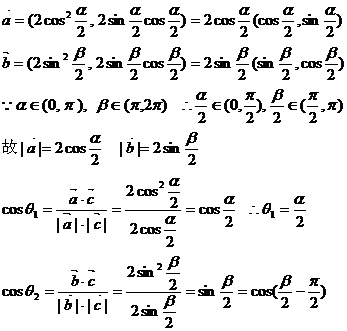
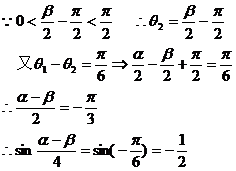
4.平面直角坐标系内有点P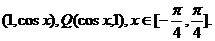
(Ⅰ)求向量 的夹角
的夹角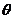 的余弦用x表示的函数
的余弦用x表示的函数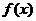 ;
;
(Ⅱ)求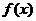 的最小值.
的最小值.
解:(Ⅰ)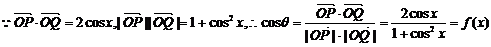
(Ⅱ)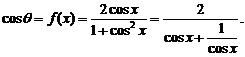
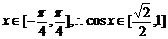 .
.
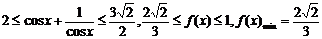 .
.
3.已知向量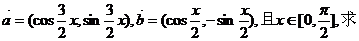
①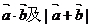 ;
;
②若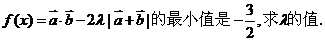
解:(1)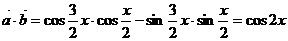
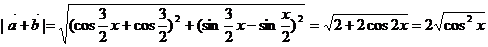
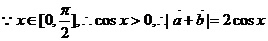
(2)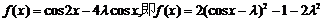
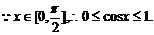
①当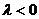 时,当县仅当
时,当县仅当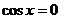 时,
时,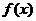 取得最小值-1,这与已知矛盾;
取得最小值-1,这与已知矛盾;
②当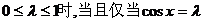 时,
时,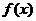 取得最小值
取得最小值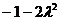 ,由已知得
,由已知得
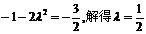 ;
;
③当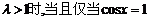 时,
时,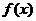 取得最小值
取得最小值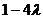 ,由已知得
,由已知得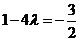
解得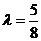 ,这与
,这与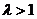 相矛盾,综上所述,
相矛盾,综上所述,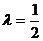 为所求。
为所求。
2.已知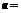
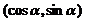 ,
,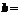
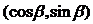 (
(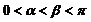 ),且|
),且|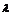
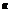
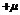
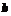 |=|
|=|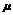
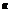
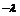
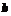 |(
|(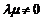 ),则
),则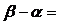
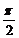 .
.
1.将函数y=f(x)·cosx的图象按向量a=(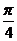 ,1)平移,得到函数y=2sin2x的图象那么函数
,1)平移,得到函数y=2sin2x的图象那么函数
f(x)可以是 ( D )
A.cosx B.2cosx C.sinx D.2sinx
17. (本小题共13分)
记关于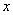 的不等式
的不等式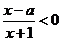 的解
的解 集为
集为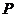 ,不等式
,不等式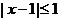 的解集为
的解集为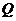 .
.
(I)若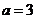 ,求
,求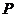 ;
;
(II)若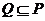 ,求正数
,求正数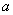 的取值范围.
的取值范围.
16. (本小题共12分)
已知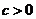 ,设P:函数
,设P:函数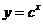 在R上单调递减,Q:不等式
在R上单调递减,Q:不等式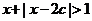 的解集为R
的解集为R
如果P和Q有且仅有一个正确,求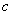 的取值范围
的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com