
2.到鸦片战争爆发前夕,中国古代政治制度就政体而论有 ( )
A.宗法制和中央集权制 B.分封制和中央集权制
C.地主制和农民政权 D.奴隶制贵族专权和封建地主阶级专政
1.元朝的行省制度实质上是继承和发展了 ( )
A.分封制 B.察举制 C.郡县制 D.三省六部制
16.已知在三角形ABC中,∠A、∠B、∠C成等差数列,|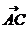 |=2
|=2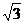 ,
,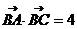
(1)求三角形ABC的面积;
(2)求三角形ABC的周长。
15. 已知向量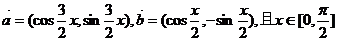 ,求
,求
①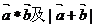 ;
;
②若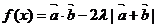 的最小值是
的最小值是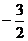 ,求实数
,求实数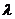 的值;
的值;
解:①a·b=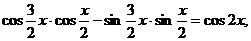
| a+b|=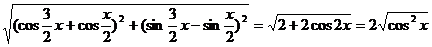 ,
,
∵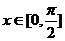 ,
∴
,
∴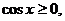 ∴| a+b|=2cosx.
∴| a+b|=2cosx.
②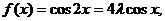 即
即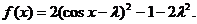
∵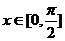 , ∴
, ∴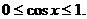
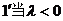 时,当且仅当
时,当且仅当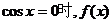 取得最小值-1,这与已知矛盾.
取得最小值-1,这与已知矛盾.
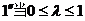 时,当且仅当
时,当且仅当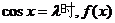 取最小值
取最小值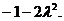
由已知得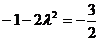 ,解得
,解得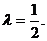
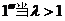 时,当且仅当
时,当且仅当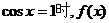 取得最小值
取得最小值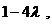
由已知得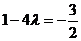 ,解得
,解得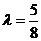 ,这与
,这与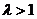 相矛盾.
相矛盾.
综上所述,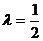 为所求.
为所求.
14. 已知平面向量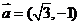 ,
,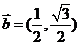 ,若存在非零实数
,若存在非零实数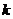 和角
和角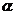 ,
,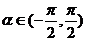 ,使得
,使得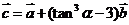 ,
,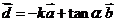 ,且
,且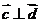 。
。
⑴若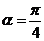 时,求
时,求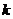 的值;
的值;
⑵若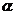 在
在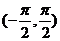 上变化时,求
上变化时,求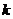 的极大值。
的极大值。
解:⑴∵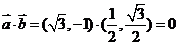
从而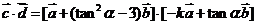 =
=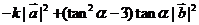
=
则 而
而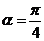 于是∴
于是∴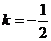
⑵令 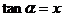 ,则
,则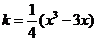 ,求导有:
,求导有:
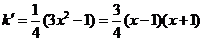
在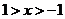 时,
时,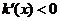 ,
,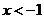 或
或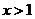 时,
时,
∴在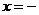 时,
时,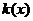 取极大值,
取极大值,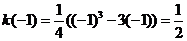
因此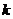 的极大值为
的极大值为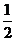
13.已知=(sinA,cosA), =(cosC,sinC),若·=sin2B, ,的夹角为θ,且A、B、C为三角形ABC的内角。
求(1)∠B (2)cos
解:(1)由·=sin2B得
sinAcosC+cosAsinC=2sinBcosB
所以 sin(A+C)=2sinBcosB
又在△ABC中,A+C=π-B,sin(A+C)≠0
所以sinB=2sinBcosB
即:cosB=,所以B=
(2)cosθ===sin(A+C)
∵在△ABC中,B=,A+C=
∴cosθ=sin=
∴cos2===
∵0<θ<π,∴cos=
12.已知向量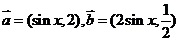 ,
,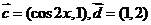 ,又二次函数
,又二次函数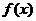 的开口向上,其对称轴为
的开口向上,其对称轴为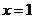 ,当
,当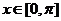 时,求使不等式
时,求使不等式 成立的
成立的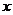 的范围。
的范围。
.依题意有,当x≥1时,f(x)是增函数
∵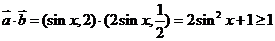
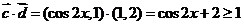
∴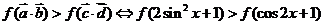
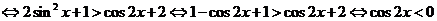
∵0≤x≤π  即为所求
即为所求
11.已知向量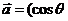 ,
,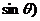 ,
,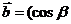 ,
,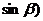 ,且
,且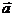 与
与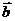 之间有关系式:
之间有关系式: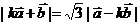 ,其中k>0.
,其中k>0.
(1)试用k表示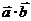 ;
;
(2)求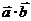 的最小值,并求此时
的最小值,并求此时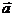 与
与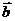 的夹角
的夹角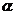 的值.
的值.
(1)因为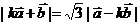 ,所以
,所以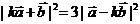 ,
,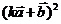
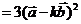 ,
,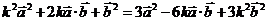 ,
,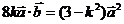
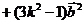 ,
,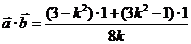
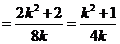 . (2)由(1)
. (2)由(1)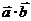
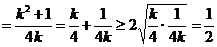 ,当且仅当
,当且仅当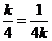 ,即
,即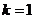 时取等号.此时,
时取等号.此时,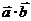
 ,
,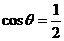 ,
,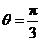 ,所以
,所以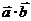 的最小值为
的最小值为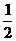 ,此时
,此时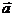 与
与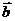 的夹角
的夹角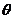 为
为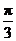
10. 已知向量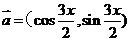 ,
, ,且
,且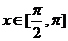
(1) 求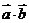 及
及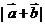 ;
;
(2) 求函数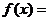
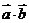 +
+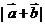 的最大值,并求使
函数 取得最大值的x的值。
的最大值,并求使
函数 取得最大值的x的值。
解(1)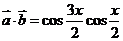 -
-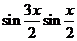 =
=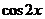
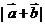 =
=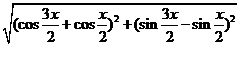
=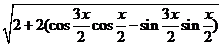
=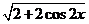 =2|
=2|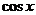 |
|
∵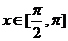
∴ 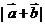 =-2
=-2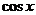
(2)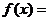
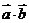 +
+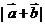 =
=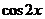 -2
-2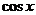
=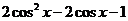
=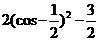
∵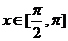
∴-1≤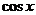 ≤0 ∴-1≤
≤0 ∴-1≤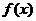 ≤3
≤3
∴当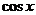 =-1时
=-1时
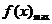 =3,此时
=3,此时 (∵
(∵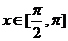 )。
)。
9.如图:已知△OFQ的面积为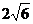 ,且
,且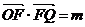 ,
,
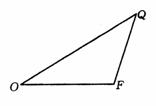
(1)若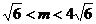 时,求向量
时,求向量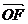 与
与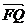 的夹角
的夹角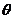 的取值范围;
的取值范围;
(2)设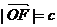 ,
,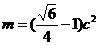 时,若以O为中心,F为焦点的双曲线经过点Q,当
时,若以O为中心,F为焦点的双曲线经过点Q,当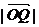 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
(1)
由已知,得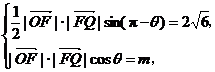 所以
所以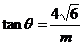 ,因为
,因为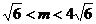 ,所以
,所以 ,则
,则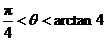 . (2)以O为原点,
. (2)以O为原点,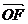 所在直线为x轴建立直角坐标系,设所求的双曲线方程为
所在直线为x轴建立直角坐标系,设所求的双曲线方程为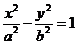 ,(a>0,b>0),Q点的坐标为(
,(a>0,b>0),Q点的坐标为(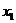 ,
,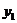 ),则
),则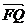 =(
=(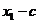 ,
,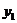 ),因为△OFQ的面积
),因为△OFQ的面积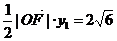 ,所以
,所以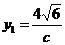 ,又由
,又由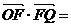 (c,0)(
(c,0)(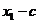 ,
,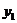 )
)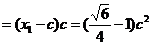 ,所以
,所以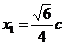 ,
,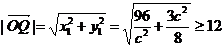 ,当且仅当c=4时,
,当且仅当c=4时,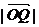 最小,此时Q的坐标为(
最小,此时Q的坐标为(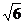 ,
,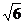 ),由此可得
),由此可得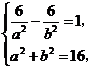 解之得
解之得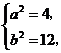 故所求的方程为
故所求的方程为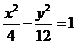
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com