
16、求数列{an}的最大、最小项的方法(函数思想):
①an+1-an=……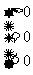 如an= -2n2+29n-3 ②
如an= -2n2+29n-3 ②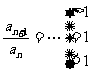 (an>0)
如an=
(an>0)
如an=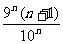 ③ an=f(n) 研究函数f(n)的增减性 如an=
③ an=f(n) 研究函数f(n)的增减性 如an=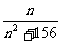
15、求和常法:公式、分组、裂项相消、错位相减、倒序相加.关键找通项结构.
分组法求数列的和:如an=2n+3n 、错位相减法求和:如an=(2n-1)2n、裂项法求和:如求和:
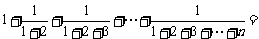 (答:
(答: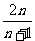 )、倒序相加法求和:
)、倒序相加法求和:
14、等差数列{an},项数2n时,S偶-S奇=nd;项数2n-1时,S奇-S偶=an ; 项数为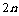 时,则
时,则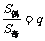 ;项数为奇数
;项数为奇数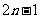 时,
时,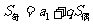 .
.
13、等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等差数列。
等比数列{an}的任意连续m项的和且不为-1时构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等比数列。如:公比为-1时,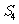 、
、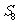 -
-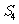 、
、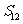 -
-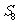 、…不成等比数列
、…不成等比数列
12、常见和: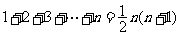
11、常用性质:等差数列中, an=am+
(n-m)d, 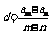 ;当m+n=p+q,am+an=ap+aq;
;当m+n=p+q,am+an=ap+aq;
等比数列中,an=amqn-m;
当m+n=p+q ,aman=apaq;如(1)在等比数列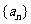 中,
中,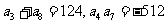 ,公比q是整数,则
,公比q是整数,则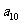 =___(答:512);(2)各项均为正数的等比数列
=___(答:512);(2)各项均为正数的等比数列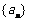 中,若
中,若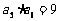 ,则
,则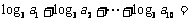 (答:10)。
(答:10)。
10、常见数列:{an}、{bn}等差则{kan+tbn}等差;{an}、{bn}等比则{kan}(k≠0)、 、{anbn}、
、{anbn}、 等比;{an}等差,则
等比;{an}等差,则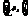 (c>0)成等比.{bn}(bn>0)等比,则{logcbn}(c>0且c
(c>0)成等比.{bn}(bn>0)等比,则{logcbn}(c>0且c 1)等差。
1)等差。
9、你能求一般数列中的最大或最小项吗?如(1)等差数列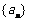 中,
中,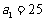 ,
,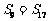 ,问此数列前多少项和最大?并求此最大值。(答:前13项和最大,最大值为169);(2)若
,问此数列前多少项和最大?并求此最大值。(答:前13项和最大,最大值为169);(2)若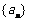 是等差数列,首项
是等差数列,首项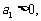
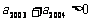 ,
,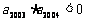 ,则使前n项和
,则使前n项和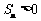 成立的最大正整数n是
(答:4006)
成立的最大正整数n是
(答:4006)
8、
首项正的递减(或首项负的递增)等差数列前n项和最大(或最小)问题,转化为解不等式 ,或用二次函数处
,或用二次函数处
7、熟记等差、等比数列的定义,通项公式,前n项和公式,在用等比数列前n项和公式时,勿忘分类讨论思想;如若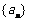 是等比数列,且
是等比数列,且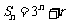 ,则
,则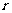 = (答:-1)
= (答:-1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com