
12.(2010年扬州调研)某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(2)若年销售量T关于x的函数为T=3240(-x2+2x+),则当x为何值时,本年度的年利润最大?最大利润为多少?
解:(1)由题意得:上年度的利润为(13-10)×5000=15000万元;
本年度每辆车的投入成本为10×(1+x)万元;
本年度每辆车的出厂价为13×(1+0.7x)万元;
本年度年销售量为5000×(1+0.4x)辆.
因此本年度的利润为
y=[13×(1+0.7x)-10×(1+x)]×5000×(1+0.4x)=(3-0.9x)×5000×(1+0.4x)=-1800x2+1500x+15000(0<x<1).
由-1800x2+1500x+15000>15000,解得0<x<.
为使本年度的年利润比上年度有所增加,则0<x<.
(2)本年度的利润为
f(x)=[13×(1+0.7x)-10×(1+x)]×3240×(-x2+2x+)=3240×(0.9x3-4.8x2+4.5x+5),
则f′(x)=3240×(2.7x2-9.6x+4.5)=972(9x-5)(x-3).
令f′(x)=0,解得x=或x=3(舍去).
当x∈(0,)时,f′(x)>0,f(x)是增函数;
当x∈(,1)时,f′(x)<0,f(x)是减函数.
∴当x=时,f(x)取得最大值,f(x)max=f()=20000.
即当x=时,本年度的年利润最大,最大利润为20000万元
11.已知某企业原有员工2000人,每人每年可为企业创利润3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,若待岗员工人数为x,则留岗员工每人每年可为企业多创利润(1-)万元.为使企业年利润最大,应安排多少员工待岗?
解:设重组后,该企业年利润为y万元.依题意得
y=(2000-x)(3.5+1-)-0.5x=-5(x+)+9000.81,
∴y=-5(x+)+9000.81(0<x≤100且x∈N),
y=-5(x+)+9000.81≤-5×2+9000.81=8820.81,
∴当且仅当x=,即x=18时取等号,此时y取得最大值.
即为使企业年利润最大,应安排18人待岗.
10.(2010年黑龙江哈尔滨模拟)某商场在促销期间规定:商场内所有商品按标价的80%出售.同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:,
|
消费金额(元)的范围 |
[200,400) |
[400,500) |
[500,700) |
[700,900) |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
130 |
… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).设购买商品的优惠率=.试问:
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800)(元)的商品,顾客购买标价为多少元的商品时,可得到不小于的优惠率?
解:(1)=,即顾客得到的优惠率是.
(2)设商品的标价为x元,则500≤x<800.则消费金额满足400≤0.8x<640.
当400≤0.8x<500,即500≤x<625时,由≥解得x≤450,不合题意;当500≤0.8x<640.即625≤x<800时,由≥解得625≤x≤725.
因此,当顾客购买标价在[625,725](元)内的商品时,可得到不小于的优惠率.
9.(2010年浙江省宁波市十校高三联考)定义域为R的函数f(x)=若关于x的函数h(x)=f2(x)+bf(x)+有5个不同的零点x1,x2,x3,x4,x5,则x12+x22+x32+x42+x52等于________.
解析:假设关于t的方程t2+bt+=0不存在t=1的根,则使h(x)=0的f(x)的值也不为1,而显然方程f(x)=k且k≠1的根最多有两个,而h(x)是关于f(x)的二次函数,因此方程h(x)=0的零点最多有四个,与已知矛盾,可见t=1时t2+bt+=0,即得b=-,所以h(x)=f 2(x)-f(x)+=(f(x)-1)(2f(x)-1),而方程f(x)-1=0的解为x=0,1,2,方程2f(x)-1=0的解为x=-1,3,由此可见五根分别为-1,0,1,2,3,因此直接计算得上述五数的平方和为15.答案:15
8.在不考虑空气阻力的情况下,火箭的最大速度v m/s和燃料的质量M kg,火箭(除燃料外)的质量m kg的函数关系是v=2000·ln(1+M/m).当燃料质量是火箭质量的________倍时,火箭的最大速度可达12 km/s.
解析:由题意得2000ln(1+)≤12000,∴≤e6-1.答案:e6-1
7.(2010年绍兴第一次质检)一位设计师在边长为3的正方形ABCD中设计图案,他分别以A、B、C、D为圆心,以b(0<b≤)为半径画圆,由正方形内的圆弧与正方形边上线段(圆弧端点在正方形边上的连线)构成了丰富多彩的图形,则这些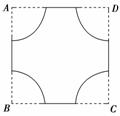 图形中实线部分总长度的最小值为________.
图形中实线部分总长度的最小值为________.
解析:由题意实线部分的总长度为l=4(3-2b)+2πb=(2π-8)b+12,l关于b的一次函数的一次项系数2π-8<0,故l关于b的函数单调递减,因此,当b取最大值时,l取得最小值,结合图形知,b的最大值为,代入上式得l最小=(2π-8)×+12=3π.答案:3π
6.(2010年苏、锡、常、镇四市调研)某市出租车收费标准如下:
起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________km.
解析:设乘客每次乘坐出租车需付费用为f(x)元,由题意可得:
 f(x) =
f(x) = 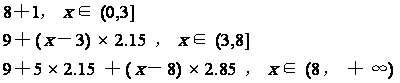
令f(x)=22.6,解得x=9.答案:9
5.某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产.已知该生产线连续生产n年的累计产量为f(n)=n(n+1)(2n+1)吨,但如果年产量超过150吨,将会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是________年.
解析:由题知第一年产量为a1=×1×2×3=3;以后各年产量分别为an=f(n)-f(n-1)=n·(n+1)(2n+1)-n·(n-1)(2n-1)=3n2(n∈N*),令3n2≤150,得1≤n≤5⇒1≤n≤7,故生产期限最长为7年.答案:7
4.(2010年珠海质检)某种细胞在培养过程中正常情况下,时刻t(单位:分钟)与细胞数n(单位:个)的部分数据如下:
|
t |
0 |
20 |
60 |
140 |
|
n |
1 |
2 |
8 |
128 |
根据表中数据,推测繁殖到1000个细胞时的时刻t最接近于________分钟.
解析:由表格中所给数据可以得出n与t的函数关系为n=2,令n=1000,得2=1000,又210=1024,所以时刻t最接近200分钟.答案:200
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com