
2. 设三次函数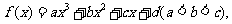 在
在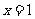 处取得极值,其图象在
处取得极值,其图象在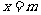 处的切线的斜率为
处的切线的斜率为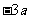 。
。
(Ⅰ)求证: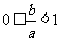 ;
;
(Ⅱ)若函数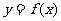 在区间
在区间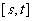 上单调递增,求
上单调递增,求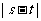 的取值范围;
的取值范围;
(Ⅲ)问是否存在实数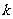 (
(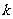 是与
是与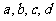 无关的常数),当
无关的常数),当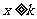 时,恒有
时,恒有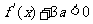 恒成立?若存在,试求出
恒成立?若存在,试求出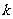 的最小值;若不存在,请说明理由。
的最小值;若不存在,请说明理由。
[例5](2009年高考北京卷文科第20题)
设数列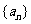 的通项公式为
的通项公式为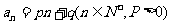 . 数列
. 数列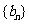 定义如下:对于正整数m,
定义如下:对于正整数m,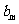 是使得不等式
是使得不等式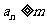 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若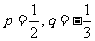 ,求
,求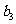 ;
;
(Ⅱ)若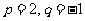 ,求数列
,求数列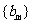 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得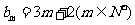 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
[解析]本题主要考查数列的概念、数列的基本性质,考查运算能力、推理论证能力、
分类讨论等数学思想方法.本题是数列与不等式综合的较难层次题.
(Ⅰ)由题意,得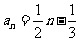 ,解
,解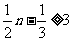 ,得
,得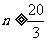 .
.
∴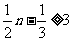 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即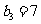 .
.
(Ⅱ)由题意,得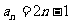 ,
,
对于正整数,由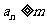 ,得
,得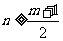 .
.
根据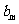 的定义可知
的定义可知
当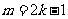 时,
时,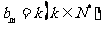 ;当
;当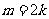 时,
时,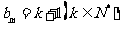 .
.
∴

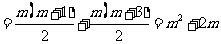 .
.
(Ⅲ)假设存在p和q满足条件,由不等式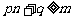 及
及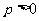 得
得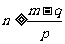 .
.
∵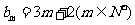 ,根据
,根据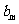 的定义可知,对于任意的正整数m 都有
的定义可知,对于任意的正整数m 都有
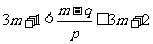 ,即
,即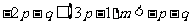 对任意的正整数m都成立.
对任意的正整数m都成立.
当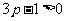 (或
(或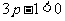 )时,得
)时,得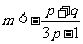 (或
(或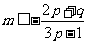 ),
),
这与上述结论矛盾!
当 ,即
,即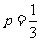 时,得
时,得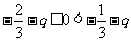 ,解得
,解得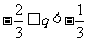 .
.
∴ 存在p和q,使得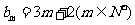 ;
;
p和q的取值范围分别是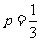 ,
,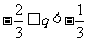 .
.
评注: 这类问题的基本特征是:要判断在某些确定条件下的某一数学对象(数值、图形、函数等)是否存在或某一结论是否成立。解决这类问题的基本策略是:通常假定题中的数学对象存在(或结论成立)或暂且认可其中的一部分的结论,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;否则,给出肯定结论。其中反证法在解题中起着重要的作用。
探索性问题是一种具有开放性和发散性的问题,此类题目的条件或结论不完备。要求解答者自己去探索,结合已有条件,进行观察、分析、比较和概括。它对学生的数学思想、数学意识及综合运用数学方法的能力提出了较高的要求。它有利于培养学生探索、分析、归纳、判断、讨论与证明等方面的能力,使学生经历一个发现问题、研究问题、解决问题的全过程。
[专题演练]
1.已知函数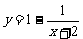 的图象按向量
的图象按向量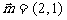 平移后便得到函数
平移后便得到函数
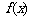 的图象,数列
的图象,数列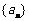 满足
满足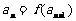 (n≥2,nÎN*).
(n≥2,nÎN*).
(Ⅰ)若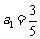 ,数列
,数列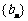 满足
满足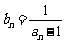 ,求证:数列
,求证:数列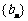 是等差数列;
是等差数列;
(Ⅱ)若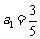 ,数列
,数列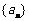 中是否存在最大项与最小项,若存在,求出最大项与最小项,若不存在,
中是否存在最大项与最小项,若存在,求出最大项与最小项,若不存在,
说明理由;
[例3](2009年高考江苏卷第14题)设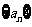 是公比为
是公比为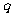 的等比数列,
的等比数列,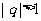 ,令
,令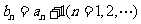 ,若数列
,若数列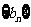 有连续四项在集合
有连续四项在集合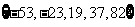 中,则
中,则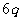 = .
= .
[解析] 考查等价转化能力和分析问题的能力。等比数列的通项。
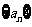 有连续四项在集合
有连续四项在集合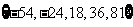 ,四项
,四项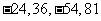 成等比数列,公比为
成等比数列,公比为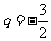 ,
,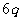 = -9
= -9
[例4](2009年高考湖北卷理科第15题)已知数列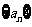 满足:
满足: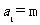 (m为正整数),
(m为正整数), 若
若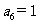 ,则m所有可能的取值为__________。
,则m所有可能的取值为__________。
[解析](1)若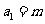 为偶数,则
为偶数,则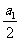 为偶, 故
为偶, 故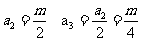
①当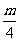 仍为偶数时,
仍为偶数时, 故
故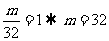
②当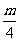 为奇数时,
为奇数时,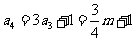
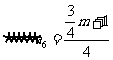
故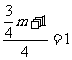 得m=4。
得m=4。
(2)若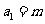 为奇数,则
为奇数,则 为偶数,故
为偶数,故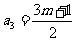 必为偶数
必为偶数
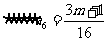 ,所以
,所以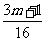 =1可得m=5
=1可得m=5
评注:这类问题的基本特征是:有条件而无结论或结论的正确与否需要确定。解决这类问题的策略是:先探索结论而后去论证结论。在探索过程中常可先从特殊情形入手,通过观察、分析、归纳、判断来作一番猜测,得出结论,再就一般情形去认证结论。
[例1](2009年高考浙江卷理科第17题)如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将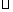 AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.

[解析]此题的破解可采用二个极端位置法,即对于F位于DC的中点时,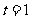 ,随着F点到C点时,因
,随着F点到C点时,因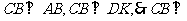 平面
平面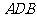 ,即有
,即有 ,对于
,对于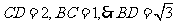 ,又
,又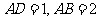 ,因此有
,因此有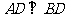 ,则有
,则有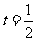 ,因此
,因此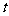 的取值范围是
的取值范围是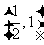 w.w.w.k.s.5.u.c.o.。m
w.w.w.k.s.5.u.c.o.。m
[例2]如图,在平面直角坐标系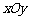 中,
中,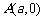
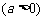 ,
,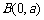 ,
,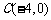 ,
,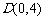 ,设
,设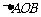 的外接圆圆心为E.
的外接圆圆心为E.
(1)若⊙E与直线CD相切,求实数a的值;
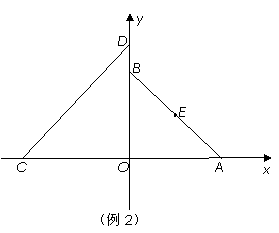 (2)设点
(2)设点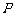 在圆
在圆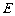 上,使
上,使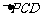 的面积等于12的点
的面积等于12的点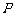 有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
[解析](1)直线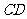 方程为
方程为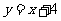 ,圆心
,圆心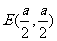 ,半径
,半径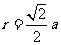 .
.
由题意得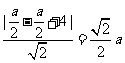 ,解得
,解得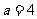 .
.
(2)∵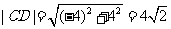 ,
,
∴当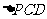 面积为
面积为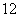 时,点
时,点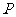 到直线
到直线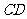 的距离为
的距离为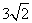 ,
,
又圆心E到直线CD距离为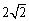 (定值),要使
(定值),要使 的面积等于12的点
的面积等于12的点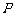 有且只有三个,只须圆E半径
有且只有三个,只须圆E半径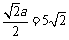 ,解得
,解得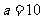 ,
,
此时,⊙E的标准方程为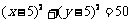 .
.
评注:这类问题的基本特征是:针对一个结论,条件未知需探索,或条件增删需确定,或条件正误需判断。解决这类问题的基本策略是:执果索因,先寻找结论成立的必要条件,再通过检验或认证找到结论成立的充分条件。在“执果索因”的过程中,常常会犯的一个错误是不考虑推理过程的可逆与否,误将必要条件当作充分条件,应引起注意。
7. 如图,在四棱锥
如图,在四棱锥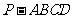 中,底面
中,底面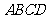 是矩形,
是矩形,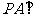 平面
平面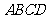 ,
,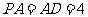 ,
,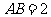 .以
.以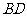 的中点
的中点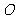 为球心、
为球心、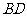 为直径的球面交
为直径的球面交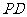 于点
于点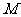 .
.
(1)求证:平面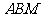 ⊥平面
⊥平面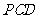 ;
;
(2)求直线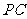 与平面
与平面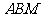 所成的角;
所成的角;
(3)求点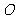 到平面
到平面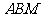 的距离.
的距离.
6. 如图,在三棱锥
如图,在三棱锥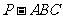 中,⊿
中,⊿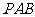 是等边三角形,
是等边三角形,
∠PAC=∠PBC=90 º
(Ⅰ)证明:AB⊥PC
(Ⅱ)若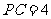 ,且平面
,且平面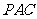 ⊥平面
⊥平面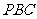 ,
,
求三棱锥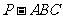 体积.
体积.
5.一个棱锥的三视图如图,则该棱锥的全面积(单位: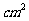 )为
)为
(A) (B)
(B)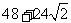
(C) (D)
(D)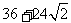
4. 设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C的面积等于
设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C的面积等于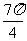 ,则球O的表面积等于
.
,则球O的表面积等于
.
3.一空间几何体的三视图如图所示,则该几何体的体积为( )
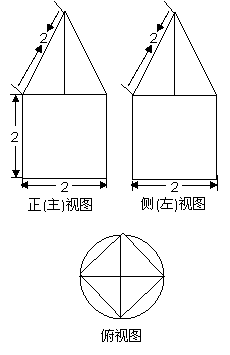

A.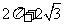 B.
B. 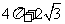 C.
C.
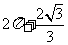 D.
D.
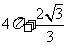
2. 给定空间中的直线l及平面a,条件“直线l与平面a内无数条直线都垂直”是“直线l与平面a垂直”的( )条件
A.充要 B.充分非必要 C.必要非充分 D.既非充分又非必要
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com