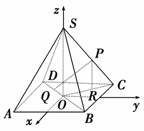
12．在正四棱锥S－ABCD中，底面边长为a，侧棱长也为a，以底面中心O为坐标原点，建立如图所示的空间直角坐标系，P点在侧棱SC上，Q点在底面ABCD的对角线BD上，试求P、Q两点间的最小距离．

解：由于S－ABCD是正四棱锥，所以P点在底面上的射影R在OC上，又底面边长为a，所以OC＝a，

而侧棱长也为a，所以SO＝OC，于是PR＝RC，故可设P点的坐标为(－x，x，a－x)(x>0)，又Q点在底面ABCD的对角线BD上，所以可设Q点的坐标为(y，y,0)，因此P、Q两点间的距离PQ＝

＝ ，显然当x＝，y＝0时d取得最小值，d的最小值等于，这时，点P恰好为SC的中点，点Q恰好为底面的中心．

11．已知A(1,2，－1)，B(2,0,2)．

(1)在x轴上求一点P，使|PA|＝|PB|；

(2)在xOz平面内的点M到A点与到B点等距离，求M点的轨迹．

解：(1)设P(a,0,0)，则由已知，得＝，

即a²－2a+6＝a²－4a+8.解得a＝1.所以P点坐标为(1,0,0)．

(2)设M(x,0，z)，则有＝.

整理得2x+6z－2＝0，即x+3z－1＝0.

故M点的轨迹是xOz平面内的一条直线．

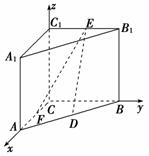
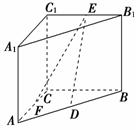
10．如图所示，直三棱柱ABC－A₁B₁C₁中，|C₁C|＝|CB|＝|CA|＝2，AC⊥CB，D、E分别是棱AB、B₁C₁的中点，F是AC的中点，求DE、EF的长度．

解：以点C为坐标原点，CA、CB、CC₁所在直线为x轴、y轴、z轴，建立如图所示的空间直角坐标系．

∵|C₁C|＝|CB|＝|CA|＝2，

∴C(0,0,0)，A(2,0,0)，B(0,2,0)，C₁(0,0,2)，B₁(0,2,2)，

由中点坐标公式可得，

D(1,1,0)，E(0,1,2)，F(1,0,0)，

∴|DE|＝＝，

|EF|＝＝.

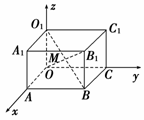
9．如图所示，在长方体OABC－O₁A₁B₁C₁中，OA＝2，AB＝3，AA₁＝2，M是OB₁与BO₁的交点，则M点的坐标是______．

解析：∵OA＝2，AB＝3，AA₁＝2，

∵A(2,0,0)，A₁(2,0,2)，B(2,3,0)，故B₁(2,3,2)．∴M点的坐标为(，，)，即M(1,1.5,1)．

答案：(1,1.5,1)

8．已知ABCD为平行四边形，且A(4,1,3)、B(2，－5,1)，C(3,7，－5)，则顶点D的坐标为________．

解析：由平行四边形中对角线互相平分的性质知，AC的中点即为BD的中点，AC的中点O(，4，－1)，设D(x，y，z)，则＝，4＝，－1＝，

∴x＝5，y＝13，z＝－3，故D(5,13，－3)．

7．在空间直角坐标系中，正方体ABCD－A₁B₁C₁D₁的顶点A(3，－1,2)，其中心M的坐标为(0,1,2)，则该正方体的棱长为__________．

解析：由A(3，－1,2)，中心M(0,1,2)所以C₁(－3,3,2)．正方体的体对角线长为AC₁＝＝2，所以正方体棱长为＝.答案：

6．在空间直线坐标系中，方程x²－4(y－1)²＝0表示的图形是__________．

解析：x²－4(y－1)²＝0化为[x－2(y－1)][x+2(y－1)]＝0，∴x－2y+2＝0或x+2y－2＝0，表示两个平面．答案：两个平面

5．在z轴上与点A(－4,1,7)和点B(3,5，－2)等距离的点C的坐标为 ______.

解析：设z轴上的点为(0,0，z)，则根据题意有

＝，

则17+49－14z＝9+25+4+4z，∴z＝.故该点是(0,0，)．

4．(2010年江苏宜兴模拟)已知B是点A(3,7，－4)在xOy平面上的射影，则²等于______．

解析：A在xOy平面上射影为B(3,0，－4)，则＝(3,0，－4)，²＝25.

3．正方体不在同一表面上的两顶点A(－1,2，－1)，B(3，－2,3)，则正方体的体积为______．

解析：设棱长为a，则a＝，∴a＝4，∴V＝64.