
8.
已知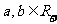 ,且
,且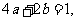 那么
那么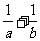 的最小值为( )
的最小值为( )
A.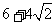 B.
B.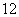 C.
C. D.
D.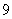
7. 甲、乙、丙三名射箭运动员在某次测试中各射箭12次,三人的测试成绩如下表
|
甲的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
3 |
3 |
3 |
3 |
|
乙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
4 |
2 |
2 |
4 |
|
丙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
2 |
4 |
4 |
2 |
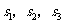 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
A.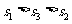 B.
B.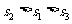 C.
C.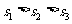 D.
D.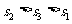
6.
某事件A发生的概率为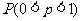 ,则事件A在一次试验中发生的次数
,则事件A在一次试验中发生的次数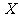 的方差的最大值为( )
的方差的最大值为( )
A.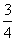 B.
B.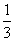 C.
C.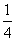 D.
D.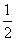
5. 矩形对角线相等,正方形是矩形,根据“三段论”推理出一个结论,则这个结论是( )
A.正方形的对角线相等 B.平行四边形的对角线相等
C.正方形是平行四边形 D.其它
4.
如果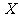 是离散型随机变量,
是离散型随机变量,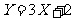 ,那么( )
,那么( )
A.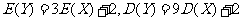 B.
B.
C.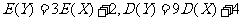 D.
D.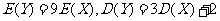
3.
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则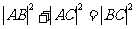 ”拓展到空间,类比平面几何的勾股定理,“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直,则可得” ( )
”拓展到空间,类比平面几何的勾股定理,“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直,则可得” ( )
A.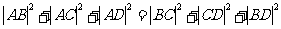
B.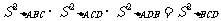
C.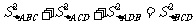
D.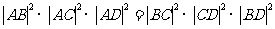
2.
某服务部门有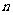 个服务对象,每个服务对象是否需要服务是独立的,若每个服务对象一天中需要服务的可能性是
个服务对象,每个服务对象是否需要服务是独立的,若每个服务对象一天中需要服务的可能性是 ,则该部门一天平均需服务的对象个数是( )
,则该部门一天平均需服务的对象个数是( )
A.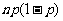 B.
B.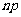 C.
C.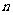 D.
D.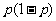
1.
不等式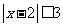 的解集为( )
的解集为( )
A.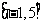 B.
B.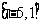 C.
C. 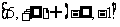 D.
D.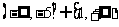
22.(本小题满分12分)
已知函数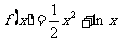
(1)若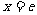 为
为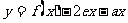 的极值点,求实数
的极值点,求实数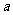 的值
的值
(2)若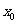 是函数
是函数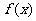 的一个零点, 且
的一个零点, 且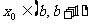 , 其中
, 其中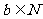 , 则求
, 则求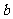 的值
的值
(3)若当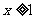 时
时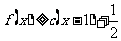 ,求
,求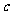 的取值范围
的取值范围
哈三中2009-2010学年度下学期
21. (本小题满分12分)
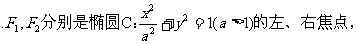 直线
直线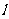 与C相交于A,B两点
与C相交于A,B两点
(1) 若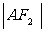 ,
,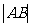 ,
,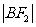 成等差数列,直线
成等差数列,直线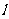 斜率为1且过
斜率为1且过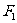 ,求a值
,求a值
(2) 若直线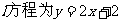 ,且
,且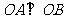 ,求a值
,求a值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com