
21.(本小题满分14分)
设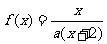 ,方程
,方程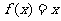 有唯一解,已知
有唯一解,已知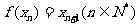 ,且
,且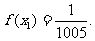
(1)求数列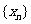 的通项公式;
的通项公式;
(2)若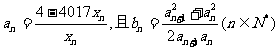 ,求和
,求和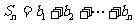 ;
;
(3)问:是否存在最小整数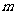 ,使得对任意
,使得对任意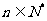 ,有
,有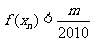 成立,若存在,求出
成立,若存在,求出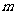 的值;若不存在,说明理由。
的值;若不存在,说明理由。
20.(本题满分14分)已知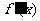 是
是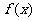 的导函数,
的导函数, ,且函数
,且函数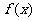 的图象过点(0,-2)。
的图象过点(0,-2)。
(1)求函数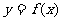 的表达式;
的表达式;
(2)设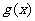 在点
在点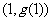 处的切线与
处的切线与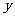 轴垂直,求
轴垂直,求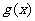 的极大值。
的极大值。
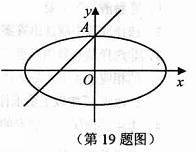
19.(本小题满分14分)如图所示,椭圆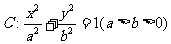 的离心率为
的离心率为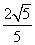 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
 (2)过点A作斜率为1的直线
(2)过点A作斜率为1的直线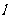 ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线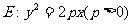 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线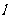 距离的最小值。
距离的最小值。
18.(本题满分14分)如图,在底 面是菱形的四棱锥S-ABCD中,SA=AB=2,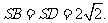
(1)证明: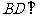 平面SAC;
平面SAC;
(2)问:侧棱SD上是否存在点E,使得SB//平面ACD?请证明你的结论;
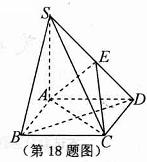 (3)若
(3)若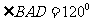 ,求几何体A-SBD的体积。
,求几何体A-SBD的体积。
17.(本小题满分12分)第16届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
|
|
喜爱运 动 动 |
不喜爱运动 |
总计 |
|
男 |
10 |
|
16 |
|
女 |
6 |
|
14 |
|
总计 |
|
|
30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志原者中(其中恰有4人会外语),抽取2名负责翻译工作,则抽出的志愿者中2人都能胜任翻译工作的概率是多少?
参考公式: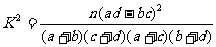 ,其中
,其中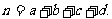
参考数据:
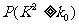 |
0.40 |
0.25 |
0.10 |
0.010 |
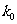 |
0.708 |
1.323 |
2.706 |
6.635 |
16.(本小题满分12分)已知函数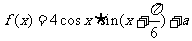 的最大值为2。
的最大值为2。
(1)求 的值及
的值及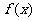 的最小正周期;
的最小正周期;
(2)求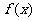 的单调递增区间。
的单调递增区间。
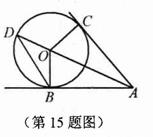
15.(几何证明选讲选做题)如右图所示,AC和AB分别是圆O的切线,
且OC=3,AB+4,延长AO到D点,则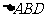 的面积是
。
的面积是
。
14.(极坐标与参数方程选做题)已知曲线C的极坐标方程是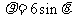 ,以极点为平在直角坐标系的原点,极轴为
,以极点为平在直角坐标系的原点,极轴为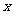 的正半轴,建立平面直角坐标系,直线
的正半轴,建立平面直角坐标系,直线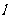 的参数方程是
的参数方程是
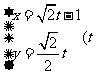 为参数),则直线
为参数),则直线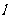 与曲线C相交所得的弦
与曲线C相交所得的弦
的弦长为 。
13.已知函数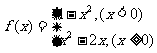 ,方程
,方程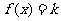 有三个
有三个
实根,由 取值范围是 。
取值范围是 。
12.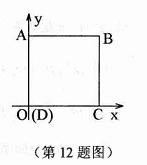 如右图
如右图 所示,一个水平放置的正方形ABCD,它在直角坐标
所示,一个水平放置的正方形ABCD,它在直角坐标
系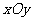 中,点B的坐标为(2,2),则在用斜二测画法画出的
中,点B的坐标为(2,2),则在用斜二测画法画出的
正方形的直观图 中,顶点
中,顶点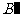 到
到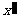 轴的距离为
。
轴的距离为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com