
(13)高三某班有50名学生,其中男生30人,女生20人,为了调查这50名学生的身体状况,现采取分层抽样的方法,抽取一个容量为20的样本,则男生被抽取的人数是 人。
(14)若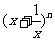 展开式的二项式系数之和为64,则展开式的常数项为 。
展开式的二项式系数之和为64,则展开式的常数项为 。
(15)若球 的表面积为
的表面积为 ,边长为2的正三角形ABC的三个顶点在球
,边长为2的正三角形ABC的三个顶点在球 的表面上,则球心
的表面上,则球心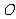 到平面ABC的距离为 。
到平面ABC的距离为 。
(16)已知抛物线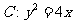 的焦点为
的焦点为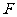 ,
,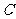 上的点
上的点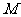 在
在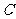 的准线上的射影为
的准线上的射影为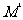 ,若
,若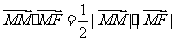 ,则点
,则点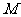 的横坐标为 。
的横坐标为 。
3. 第Ⅱ卷共10小题,共90分。
(1) 不等式|x+1|-2>0的解集是
(A)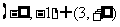 (B)
(B)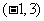
(C)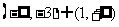 (D)
(D)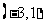
(2)
已知函数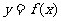 的反函数
的反函数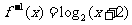 ,则方程
,则方程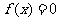 的跟为
的跟为
(A)1 (B)0 (C)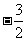 (D)2
(D)2
(3)
已知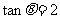 则
则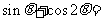
(A)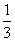 (B)
(B)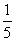 (C)
(C)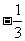 (D)
(D)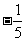
(4)
已知向量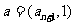 ,
,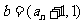 ,
,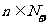 ,且
,且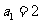 ,
,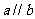 ,则数列
,则数列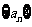 的前5项和为
的前5项和为
(A)10 (B)14 (C)20 (D)27
(5)
椭圆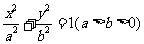 的离心率是
的离心率是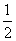 ,则
,则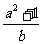 的最小值为
的最小值为
(A)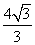 (B)
(B)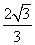 (C)
(C)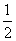 (D)1
(D)1
(6)
设m, n为两条不同的直线,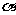 ,
,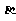 为两个不同的平面,则
为两个不同的平面,则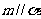 的一个充分条件是
的一个充分条件是
(A)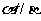 且
且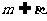 (B)
(B)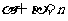 且
且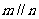
(C)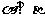 且
且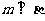 (D)
(D)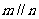 且
且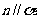
(7)
过点A(0,3),且被圆(x-1)2+y2=4截得的弦长为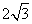 的直线方程是
的直线方程是
(A)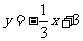 (B)
(B)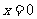 或
或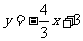
(C)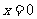 或
或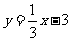 (D)
(D)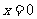 或
或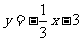
(8)
在坐标平面上,不等式组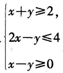 ,所表示的平面区域的面积为
,所表示的平面区域的面积为
(A)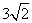 (B)
(B)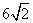 (C)6 (D)3
(C)6 (D)3
(9) 某班要从6名男生、4名女生中选派6人参加某次社区服务,,要求女生甲、乙要么都参加,要么都不参加,且至少要有两名女生参加,那么不同的选派方案种数为
(A)70 (B)85 (C)105 (D)185
(10) 在正三棱柱ABC-A1B1C1中,已知AB=1,点D在棱BB1上,且BD=1,则AD与平面AA1CC1所成角的正切值为
(A)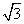 (B)1 (C)
(B)1 (C)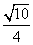 (D)
(D)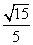
(11) 若对任意角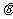 ,都有
,都有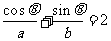 ,则下列不等式恒成立的是
,则下列不等式恒成立的是
(A)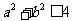 (B)
(B)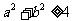
(C)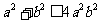 (D)
(D)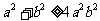
(12) 若函数y=x3-3ax+a在区间(1,2)内有极小值,则实数a的取值范围是
(A)1<a<2 (B)1<a<4
(C)2<a<4 (D)a>4或a<1
第Ⅱ卷
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。在试题卷上作答无效。
19.(15分) 已知椭圆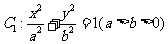 的离心率为
的离心率为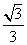 ,直线
,直线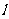 :
: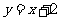 与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切.
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点F2,直线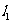 过点F1且垂直于椭圆的长轴,动直线
过点F1且垂直于椭圆的长轴,动直线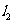 垂直
垂直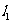 于点P,线段PF2垂直平分线交
于点P,线段PF2垂直平分线交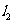 于点M,求点M的轨迹C2的方程;
于点M,求点M的轨迹C2的方程;
(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足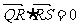 ,求
,求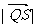 的取值范围。
的取值范围。
浙江瑞安中学09-10学年高二下学期3月月考
18.(12分) 已知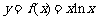 .
.
(1)求函数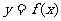 的图像在
的图像在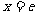 处的切线方程;
处的切线方程;
(2)设实数 ,求函数
,求函数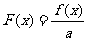 在
在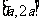 上的最大值;
上的最大值;
(3)证明对一切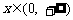 ,都有
,都有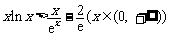 成立。
成立。
17.(8分)数列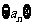 中,
中,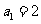 ,
,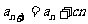 (
(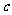 是不为零的常数,
是不为零的常数,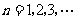 ),且
),且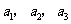 成等比数列.
成等比数列.
(1)求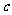 的值;
的值;
(2)求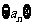 的通项公式;
的通项公式;
(3)求数列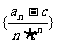 的前
的前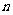 项之和
项之和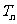 。
。
16.(5分)已知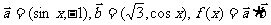
(1)若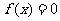 且
且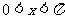 ,求
,求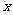 的值;
的值;
(2)求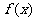 的最小正周期和单调增区间。
的最小正周期和单调增区间。
15.函数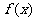 对任意实数
对任意实数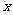 满足条件
满足条件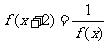 ,若
,若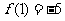 ,则
,则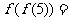 .
.
14.设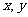 满足约束条件:
满足约束条件:
 , 则
, 则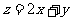 的最大值是
.
的最大值是
.
13.抛物线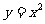 在点 处的切线平行于直线
在点 处的切线平行于直线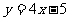 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com