
20.(本小题满分12分)
设椭圆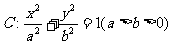 的离心率
的离心率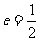 ,右焦点到直线
,右焦点到直线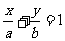 的距离
的距离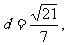 O为坐标原点。
O为坐标原点。
(I)求椭圆C的方程;
(II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值。
19.(本小题满分12分)
如图4,在直三棱柱ABC-A1B1C1中,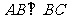 ,P为A1C1的中点,AB=BC=kPA。
,P为A1C1的中点,AB=BC=kPA。
(I)当k=1时,求证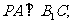
 (II)当k为何值时,直线PA与平面BB1C1C所成的角的正弦值为
(II)当k为何值时,直线PA与平面BB1C1C所成的角的正弦值为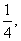 并求此时二面角A-PC-B的余弦值。
并求此时二面角A-PC-B的余弦值。
18.(本小题满分12分)
在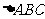 中,点M是BC的中点,
中,点M是BC的中点,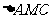 的三边长是连续三个正整数,且
的三边长是连续三个正整数,且
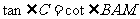
(I)判断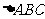 的形状;
的形状;
(II)求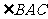 的余弦值。
的余弦值。
17.(本小题满分12分)
某选手进行n次射击训练,每次击中目标的概率为P,且每次击中目标与否是相互独立的,X记为击中目标的次数,若随机变量X的数学期望EX=3,方差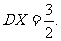
(I)求n,P的值;
(II)若这n次射击有3次或3次以上未击中目标,则需继续训练,求该选手需要继续训练的概率。
16.已知函数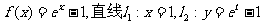
(t为常数,且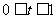 ),直线
),直线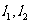 与函数
与函数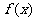 的图
的图
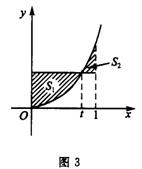
象围成的封闭图形,以及直线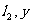 轴与函数
轴与函数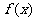 的图
的图
象围成的封闭图形如图3中阴影所示。当t变化时阴影部分
的面积的最小值为 。
14.过双曲线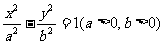 的一个焦点作一条渐近线的垂线,垂足恰好落在曲线
的一个焦点作一条渐近线的垂线,垂足恰好落在曲线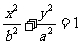 上,则双曲线的离心率为
。
上,则双曲线的离心率为
。
 15.抛掷红、蓝两颗均匀的骰子,已知点数不同,则红色骰子的点数比蓝色骰子的点数恰好多两点的概率为
。
15.抛掷红、蓝两颗均匀的骰子,已知点数不同,则红色骰子的点数比蓝色骰子的点数恰好多两点的概率为
。
13.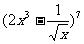 的展开式中常数项是
。
的展开式中常数项是
。
12.若关于x的不等式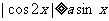 在闭区间
在闭区间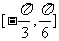 上恒成立,则实数a的取值范围是 ( )
上恒成立,则实数a的取值范围是 ( )
A.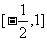 B.
B.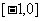 C.
C.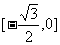 D.[0,1]
D.[0,1]
第Ⅱ卷
本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答。第(22)题~第(24)题为选考题,考生根据要求作答。
11.由0,1,2,3,4,5这六个数字组成的不重复的六位数中,不出现“135”与“24”的六位数的个数为 ( )
A.582 B.504 C.490 D.486
10.给出下列四个命题:
①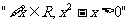 的否定是
的否定是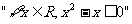 ;
;
②对于任意实数x,有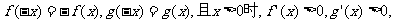
则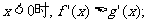
③函数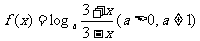 是偶函数;
是偶函数;
④若对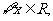 函数f(x)满足
函数f(x)满足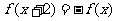 ,则4是该函数的一个周期,其中真命题的个数为 ( )
,则4是该函数的一个周期,其中真命题的个数为 ( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com