
5.总体分布的估计:用样本估计总体,是研究统计问题的一个基本思想方法,一般地,样本容量越大,这种估计就越精确,要求能画出频率分布表和频率分布直方图;
4.掌握抽样的三种方法:(1)简单随机抽样(包括抽签法和随机数表法);(2)系统抽样,也叫等距离抽样;(3)分层抽样,常用于某个总体由差异明显的几部分组成的情形;
3.记住以下重要公式和结论:
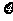 |
x1 |
X2 |
… |
xn |
… |
|
P |
P1 |
P2 |
… |
Pn |
… |
(1)期望值E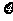 = x1p1 + x2p2 + … + xnpn + … ;
= x1p1 + x2p2 + … + xnpn + … ;
(2)方差D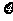 =
=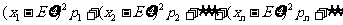 ;
;
(3)标准差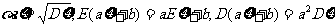 ;
;
(4)若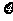 -B(n,p),则E
-B(n,p),则E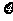 =np, D
=np, D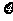 =npq,这里q=1- p;
=npq,这里q=1- p;
2.二项分布:记作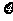 -B(n,p),其中n,p为参数,
-B(n,p),其中n,p为参数,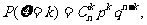 并记
并记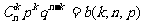 ;
;
1.理解随机变量,离散型随机变量的定义,能够写出离散型随机变量的分布列,由概率的性质可知,任意离散型随机变量的分布列都具有下述两个性质:(1)pi≥0,i=1,2,…; (2) p1+p2+…=1;
8.等可能事件的概率公式:(1)P(A)=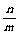 ;(2)互斥事件分别发生的概率公式为:P(A+B)=P(A)+P(B);(3)相互独立事件同时发生的概率公式为P(AB)=P(A)P(B);(4)独立重复试验概率公式Pn(k)=
;(2)互斥事件分别发生的概率公式为:P(A+B)=P(A)+P(B);(3)相互独立事件同时发生的概率公式为P(AB)=P(A)P(B);(4)独立重复试验概率公式Pn(k)=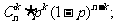 (5)如果事件A、B互斥,那么事件A与
(5)如果事件A、B互斥,那么事件A与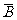 、
、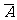 与
与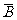 及事件
及事件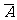 与
与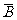 也都是互斥事件;(6)如果事件A、B相互独立,那么事件A、B至少有一个不发生的概率是1-P(AB)=1-P(A)P(B);(6)如果事件A、B相互独立,那么事件A、B至少有一个发生的概率是1-P(
也都是互斥事件;(6)如果事件A、B相互独立,那么事件A、B至少有一个不发生的概率是1-P(AB)=1-P(A)P(B);(6)如果事件A、B相互独立,那么事件A、B至少有一个发生的概率是1-P(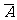

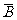 )=1-P(
)=1-P(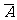 )P(
)P(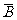 );
);
理科选修内容基本知识
7.F(x)=(ax+b)n展开式的各项系数和为f(1);奇数项系数和为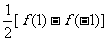 ;偶数项的系数和为
;偶数项的系数和为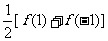 ;
;
6.二项式系数具有下列性质:
(1) 与首末两端等距离的二项式系数相等;
(2)若n为偶数,中间一项(第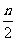 +1项)的二项式系数最大;若n为奇数,中间两项(第
+1项)的二项式系数最大;若n为奇数,中间两项(第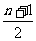 和
和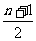 +1项)的二项式系数最大;
+1项)的二项式系数最大;
(3)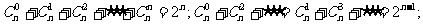
5.二项式定理:(1)掌握二项展开式的通项: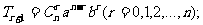
(2)注意第r+1项二项式系数与第r+1系数的区别;
4.常用性质:n.n!=(n+1)!-n!;即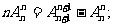
 (1≤r≤n);
(1≤r≤n);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com