
5.直线与平面所成的角
斜线和平面所成的是一个直角三角形的锐角,它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影。通常通过斜线上某个特殊点作出平面的垂线段,垂足和斜足的连线,是产生线面角的关键;
4.异面直线所成角的求法:
(1)平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;
(2)补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;
3.立平斜公式:如图,AB和平面所成的角是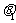 ,AC在平面内,AC和AB的射影AB成
,AC在平面内,AC和AB的射影AB成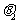 ,设∠BAC=
,设∠BAC=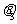 ,则cos
,则cos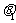 cos
cos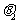 =cos
=cos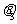 ;
;
2.


 已知:直二面角M-AB-N中,AE
已知:直二面角M-AB-N中,AE  M,BF
M,BF N,∠EAB=
N,∠EAB=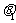 ,∠ABF=
,∠ABF=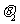 ,异面直线AE与BF所成的角为
,异面直线AE与BF所成的角为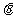 ,则
,则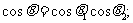
1.从一点O出发的三条射线OA、OB、OC,若∠AOB=∠AOC,则点A在平面∠BOC上的射影在∠BOC的平分线上;
13.求轨迹的常用方法:
(1)直接法:直接通过建立x、y之间的关系,构成F(x,y)=0,是求轨迹的最基本的方法;
(2)待定系数法:所求曲线是所学过的曲线:如直线,圆锥曲线等,可先根据条件列出所求曲线的方程,再由条件确定其待定系数,代回所列的方程即可;
(3)代入法(相关点法或转移法):若动点P(x,y)依赖于另一动点Q(x1,y1)的变化而变化,并且Q(x1,y1)又在某已知曲线上,则可先用x、y的代数式表示x1、y1,再将x1、y1带入已知曲线得要求的轨迹方程;
(4)定义法:如果能够确定动点的轨迹满足某已知曲线的定义,则可由曲线的定义直接写出方程;
(5)参数法:当动点P(x,y)坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将x、y均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程。
12.处理椭圆、双曲线、抛物线的弦中点问题常用代点相减法,设A(x1,y1)、B(x2,y2)为椭圆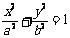 (a>b>0)上不同的两点,M(x0,y0)是AB的中点,则KABKOM=
(a>b>0)上不同的两点,M(x0,y0)是AB的中点,则KABKOM=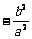 ;对于双曲线
;对于双曲线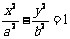 (a>0,b>0),类似可得:KAB.KOM=
(a>0,b>0),类似可得:KAB.KOM=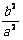 ;对于y2=2px(p≠0)抛物线有KAB=
;对于y2=2px(p≠0)抛物线有KAB=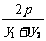
11.对于y2=2px(p≠0)抛物线上的点的坐标可设为(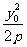 ,y0),以简化计算;
,y0),以简化计算;
10.过椭圆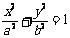 (a>b>0)左焦点的焦点弦为AB,则
(a>b>0)左焦点的焦点弦为AB,则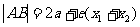 ,过右焦点的弦
,过右焦点的弦 ;
;
9.抛物线y2=2px(p>0)的焦点弦(过焦点的弦)为AB,A(x1,y1)、B(x2,y2),则有如下结论:(1)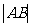 =x1+x2+p;(2)y1y2=-p2,x1x2=
=x1+x2+p;(2)y1y2=-p2,x1x2=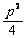 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com