
4. 求函数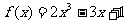 零点的个数为 ( )
零点的个数为 ( )
A. 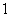 B.
B. 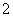 C.
C. 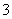 D.
D. 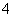
3. 若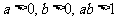 ,
,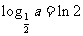 ,则
,则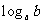 与
与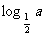 的关系是( )
的关系是( )
A. 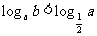 B.
B. 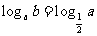
C. 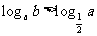 D.
D.
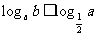
2.
已知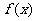 唯一的零点在区间
唯一的零点在区间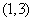 、
、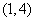 、
、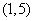 内,那么下面命题错误的( )
内,那么下面命题错误的( )
A. 函数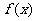 在
在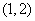 或
或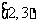 内有零点 B.
函数
内有零点 B.
函数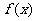 在
在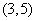 内无零点
内无零点
C.
函数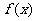 在
在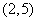 内有零点 D. 函数
内有零点 D. 函数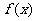 在
在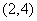 内不一定有零点
内不一定有零点
1. 若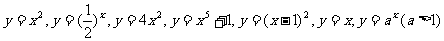 上述函数是幂函数的个数是( ) A.
上述函数是幂函数的个数是( ) A.  个 B.
个 B. 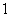 个 C.
个 C. 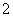 个 D.
个 D. 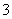 个
个
(15)(本小题共13分)www.@ks@
已知函数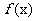
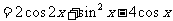 。
。
(Ⅰ)求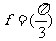 的值;
的值;
(Ⅱ)求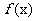 的最大值和最小值。
的最大值和最小值。
(16)(本小题共14分)
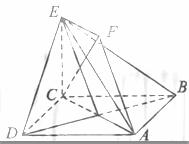
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=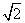 ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
(17)(本小题共13分) www.@ks@
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为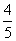 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为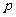 ,
,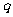 (
(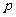 >
>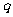 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
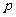 |
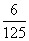 |
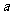 |
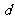 |
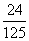 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求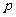 ,
,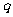 的值;
的值;
(Ⅲ)求数学期望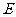 ξ。
ξ。
(18)(本小题共13分)
已知函数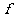 (
(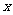 )=In(1+
)=In(1+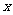 )-
)-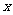 +
+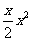 (
(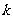 ≥0)。
≥0)。
(Ⅰ)当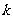 =2时,求曲线
=2时,求曲线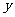 =
=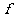 (
(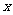 )在点(1,
)在点(1,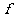 (1))处的切线方程;
(1))处的切线方程;
(Ⅱ)求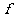 (
(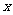 )的单调区间。
)的单调区间。
(19)(本小题共14分)www.@ks@
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于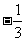 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
(20)(本小题共13分)
已知集合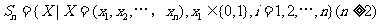 对于
对于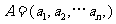 ,
,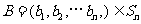 ,定义A与B的差为
,定义A与B的差为
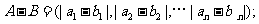
A与B之间的距离为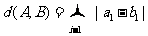
(Ⅰ)证明: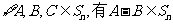 ,且
,且 ;
;
(Ⅱ)证明: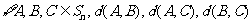 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P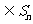 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为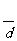 (P).
(P).
证明: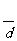 (P)≤
(P)≤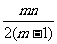 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
2010年普通高等学校招生全国统一考试
(9)在复平面内,复数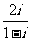 对应的点的坐标为
。
对应的点的坐标为
。
(10)在△ABC中,若b = 1,c =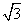 ,
,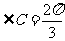 ,则a =
。
,则a =
。
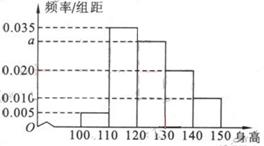 (11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
(11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
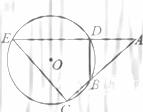
(12)如图,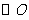 的弦ED,CB的延长线交于点A。若BD
的弦ED,CB的延长线交于点A。若BD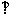 AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
 (13)已知双曲线
(13)已知双曲线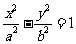 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆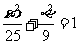 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
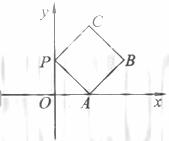
(14)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的轨迹方程是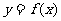 ,则
,则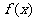 的最小正周期为
;
的最小正周期为
;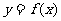 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿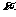 轴滚动”包括沿
轴滚动”包括沿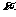 轴正方向和沿
轴正方向和沿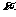 轴负方向滚动。沿
轴负方向滚动。沿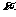 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在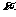 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿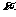 轴负方向滚动。
轴负方向滚动。
(1) 集合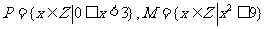 ,则
,则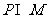 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
(2)在等比数列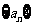 中,
中,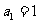 ,公比
,公比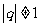 .若
.若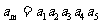 ,则m=
,则m=
(A)9 (B)10 (C)11 (D)12
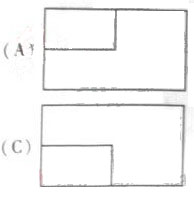
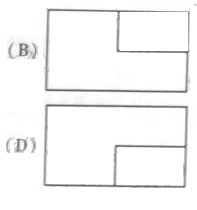
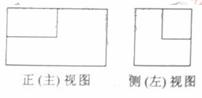 (3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为
(A)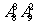 (B)
(B)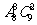 (C)
(C) 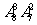 (D)
(D)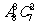
(5)极坐标方程(p-1)( )=(p
)=(p 0)表示的图形是
0)表示的图形是
(A)两个圆 (B)两条直线
(C)一个圆和一条射线 (D)一条直线和一条射线
(6)a、b为非零向量。“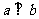 ”是“函数
”是“函数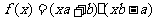 为一次函数”的
为一次函数”的
(A)充分而不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(7)设不等式组 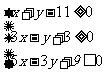 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y=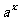 的图像上存在区域D上的点,则a 的取值范围是
的图像上存在区域D上的点,则a 的取值范围是
(A)(1,3]
(B )[2,3] (C )
(1,2]
(D )[ 3,  ]
]
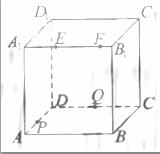 (8)如图,正方体ABCD-
(8)如图,正方体ABCD-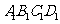 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱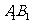 上,动点P,Q分别在棱AD,CD上,若EF=1,
上,动点P,Q分别在棱AD,CD上,若EF=1,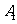 E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
(A)与x,y,z都有关
(B)与x有关,与y,z无关
(C)与y有关,与x,z无关
(D)与z有关,与x,y无关
第II卷(共110分)
第二节 书面表达(满分25分)
假如你叫华华,进入高三后一直想买一个MP3,但是母亲反对。请你根据下表中的信息,给妈妈写一封信,说服她满足你的愿望。
|
使用MP3的目的 |
承诺 |
|
1.听语文、英语课文录音 |
1.只在课外学习疲劳时和睡觉前听 |
|
2.偶尔听音乐放松大脑 |
2.作为回报,多做家务 |
注意:1.可适当增加细节,以使行文连贯;
2.词数100左右。开头及结尾已给出,不计入总词数。
Dear Mum,
As I’m in Senior 3, I strongly feel the urge to get an MP3 player, so I’m writing to you.For one thing,

Hope you’ll satisfy this request of mine.
第一节 短文改错(共10小题;每小题1分,满分10分)
假定英语课上老师要求同桌之间交换修改作文,请你修改你同学写的以下作文。文中共有10处语言错误,每句中最多有两处。错误涉及一个单词的增加、删除或修改。
增加:在缺词处加一个漏字符号(∧),并在其下面写出该加的词。
删除:把多余的词用斜线(\)划掉。
修改:在错的词下划一横线,并在该词下面写出修改后的词。
注意:1.每处错误及其修改均仅限一词;
2.只允许修改10处,多者(从第11处起)不计分。
Today is Sunday.The sky is full of sunshine, so does my life.At about 9:00 a.m, I go to the bookstore with my friends.There was a lot of new books, I didn’t know which one to buy, because these books were all useful to me.At last, I chose two.At 10:00, we went to the cinema, the film calling Titanic was very popular.It took us about 3 hours to see.Having seen the film, and everyone was deeply moved.Some friends even burst out tears.From the story, I understand that love is noble and valuable.That’s a really wonderful film.It is very worth seeing again.What a happy day! I hope tomorrow I will be even happy!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com