
4.已知长方体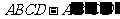 中,棱
中,棱 ,
,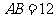 ,那么直线
,那么直线 和平面
和平面 的距离是
的距离是 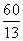 .
.
2.如果三棱锥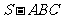 的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点
的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点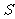 在底面的射影
在底面的射影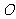 在
在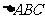 内,那么
内,那么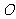 是
是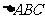 的(
的( 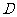 )
)
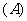 垂心
垂心
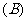 重心
重心  外心
外心 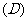 内心
内心
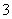 .已知三棱锥
.已知三棱锥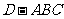 的三个侧面与底面全等,且
的三个侧面与底面全等,且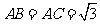 ,
,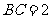 ,则以
,则以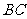 为棱,以面
为棱,以面 与面
与面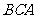 为面的二面角的大小是(
为面的二面角的大小是( 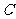 )
)
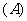
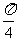
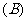
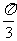
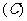
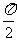
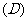
1.给出下列命题:
①底面是正多边形的棱锥是正棱锥;
②侧棱都相等的棱锥是正棱锥;
③侧棱和底面成等角的棱锥是正棱锥;
④侧面和底面所成二面角都相等的棱锥是正棱锥,
其中正确命题的个数是( 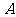 )
)
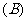
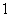
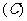
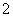
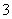
4.正棱锥的性质有
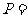 {四棱柱},
{四棱柱},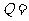 {平行六面体},
{平行六面体},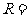 {长方体},
{长方体},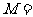 {正方体},
{正方体},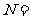 {正四棱柱},
{正四棱柱},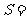 {直平行六面体},这六个集合之间的关系是
{直平行六面体},这六个集合之间的关系是
3. 叫正棱锥
2.正棱柱的性质有
1. 叫棱柱
了解棱柱和棱锥的概念,周围棱柱、正棱锥的有关性质,能进行有关角和距离的运算。
(三)例题分析:
例1.(1)设数列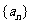 是递增等差数列,前三项的和为
是递增等差数列,前三项的和为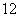 ,前三项的积为
,前三项的积为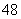 ,则它的首项为
2 .
,则它的首项为
2 .
(2)已知等差数列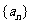 的公差
的公差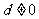 ,且
,且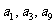 成等比数列,则
成等比数列,则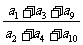
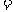
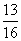 .
.
例2.有四个数,其中前三个数成等差数列,后三个数成等比数列,且第一个数与第四个数的和是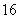 ,第二个数与第三个书的和是
,第二个数与第三个书的和是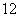 ,求这四个数.
,求这四个数.
解:设这四个数为: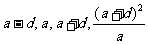 ,则
,则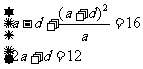
解得: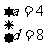 或
或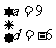 ,所以所求的四个数为:
,所以所求的四个数为: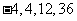 ;或
;或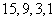 .
.
例3.由正数组成的等比数列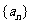 ,若前
,若前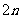 项之和等于它前
项之和等于它前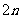 项中的偶数项之和的11倍,第3项与第4项之和为第2项与第4项之积的11倍,求数列
项中的偶数项之和的11倍,第3项与第4项之和为第2项与第4项之积的11倍,求数列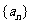 的通项公式.
的通项公式.
解:当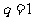 时,得
时,得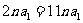 不成立,∴
不成立,∴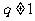 ,
,
 ∴
∴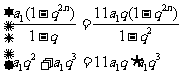
由①得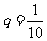 ,代入②得
,代入②得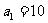 ,
,
∴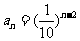 .
.
说明:用等比数列前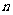 项和公式时,一定要注意讨论公比是否为1.
项和公式时,一定要注意讨论公比是否为1.
例4.已知等差数列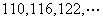 ,
,
(1)在区间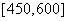 上,该数列有多少项?并求它们的和;
上,该数列有多少项?并求它们的和;
(2)在区间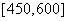 上,该数列有多少项能被
上,该数列有多少项能被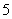 整除?并求它们的和.
整除?并求它们的和.
解: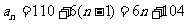 ,
,
(1)由 ,得
,得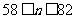 ,又
,又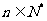 ,
,
∴ 该数列在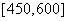 上有
上有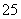 项, 其和
项, 其和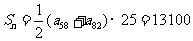 .
.
(2)∵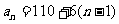 ,∴要使
,∴要使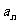 能被
能被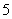 整除,只要
整除,只要 能被
能被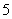 整除,即
整除,即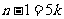 ,
,
∴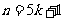 ,∴
,∴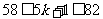 ,∴
,∴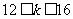 ,∴在区间
,∴在区间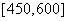 上该数列中能被
上该数列中能被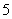 整除的项共有
整除的项共有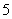 项即第
项即第 项,其和
项,其和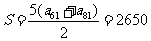 .
.
(二)主要方法:
1.涉及等差(比)数列的基本概念的问题,常用基本量 来处理;
来处理;
2.使用等比数列前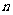 项和公式时,必须弄清公比
项和公式时,必须弄清公比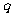 是否可能等于1还是必不等于1,如果不能确定则需要讨论;
是否可能等于1还是必不等于1,如果不能确定则需要讨论;
3.若奇数个成等差数列且和为定值时,可设中间三项为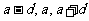 ;若偶数个成等差数列且和为定值时,可设中间两项为
;若偶数个成等差数列且和为定值时,可设中间两项为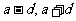 ,其余各项再根据等差数列的定义进行对称设元.若干个数个成等比数列且积为定值时,设元方法与等差数列类似.
,其余各项再根据等差数列的定义进行对称设元.若干个数个成等比数列且积为定值时,设元方法与等差数列类似.
4.在求解数列问题时要注意运用函数思想,方程思想和整体消元思想,设而不求.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com