
2.甲袋装有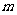 个白球,
个白球,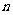 个黑球,乙袋装有
个黑球,乙袋装有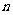 个白球,
个白球,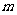 个黑球,(
个黑球,(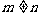 ),现从两袋中各摸一个球,
),现从两袋中各摸一个球,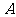 :“两球同色”,
:“两球同色”,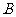 :“两球异色”,则
:“两球异色”,则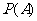 与
与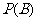 的大小关系为( )
的大小关系为( )
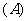
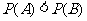
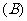
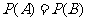
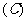
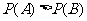
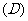 视
视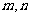 的大小而定
的大小而定
1.如果事件A、B互斥,那么 ( B )
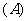 A+B是必然事件
A+B是必然事件 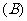
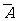 +
+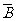 是必然事件
是必然事件
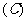
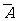 与
与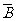 一定互斥
一定互斥
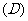
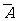 与
与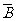 一定不互斥
一定不互斥
(四)例题分析:
例1.袋中有5个白球,3个黑球,从中任意摸出4个,求下列事件发生的概率:
(1)摸出2个或3个白球;(2)至少摸出1个白球;(3)至少摸出1个黑球.
解:从8个球中任意摸出4个共有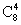 种不同的结果.记从8个球中任取4个,其中恰有1个白球为事件A1,恰有2个白球为事件A2,3个白球为事件A3,4个白球为事件A4,恰有i个黑球为事件Bi,则
种不同的结果.记从8个球中任取4个,其中恰有1个白球为事件A1,恰有2个白球为事件A2,3个白球为事件A3,4个白球为事件A4,恰有i个黑球为事件Bi,则
(1)摸出2个或3个白球的概率:
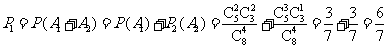
(2)至少摸出1个白球的概率P2=1-P(B4)=1-0=1
(3)至少摸出1个黑球的概率P3=1-P(A4)=1-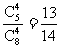
答:(1)摸出2个或3个白球的概率是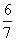 ;(2)至少摸出1个白球的概率是1;
;(2)至少摸出1个白球的概率是1;
(3)至少摸出1个黑球的概率是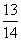 .
.
例2. 盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品;(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
解:从6只灯泡中有放回地任取两只,共有62=36种不同取法.
(1)取到的2只都是次品情况为22=4种.因而所求概率为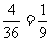 .
.
(2)由于取到的2只中正品、次品各一只有两种可能:第一次取到正品,第二次取到次品;及第一次取到次品,第二次取到正品.因而所求概率为 P=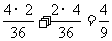
(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件.因而所求概率为 P=1-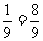
答:(1)取到的2只都是次品的概率为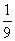 ;(2)取到的2只中正品、次品各一只的概率为
;(2)取到的2只中正品、次品各一只的概率为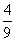 ;(3)取到的2只中至少有一只正品的概率为
;(3)取到的2只中至少有一只正品的概率为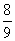 .
.
例3.从男女学生共有36名的班级中,任意选出2名委员,任何人都有同样的当选机会.如果选得同性委员的概率等于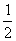 ,求男女生相差几名?
,求男女生相差几名?
解:设男生有x名,则女生有36-x名.选得2名委员都是男性的概率为
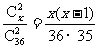
选得2名委员都是女性的概率为
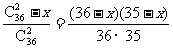
以上两种选法是互斥的,又选得同性委员的概率等于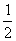 ,得
,得
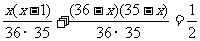 ,解得x=15或x=21
,解得x=15或x=21
即男生有15名,女生有36-15=21名,或男生有21名,女生有36-21=15名.
答:男女生相差6名.
例4.在某地区有2000个家庭,每个家庭有4个孩子,假定男孩出生率是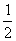 .
.
(1)求在一个家庭中至少有一个男孩的概率;
(2)求在一个家庭中至少有一个男孩且至少有一个女孩的概率;
解: (1)P(至少一个男孩)=1-P(没有男孩)=1-(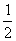 )4=
)4=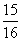 ;
;
(2)P(至少1个男孩且至少1个女孩)=1-P(没有男孩)-P(没有女孩)=1-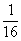 -
-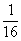 =
=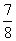 ;
;
(三)基础训练:
1.某产品分甲、乙、丙三个等级,其中乙、丙两等级为次品,若产品中出现乙级品的概率为0.03,出现丙级品的概率为0.01,则在成品中任意抽取一件抽得正品的概率为( )
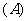 0.04
0.04
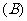 0.96
0.96
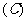 0.97
0.97 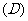 0.99
0.99
2.下列说法中正确的是 ( )
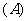 事件A、B中至少有一个发生的概率一定比A、B中恰有一个发生的概率大
事件A、B中至少有一个发生的概率一定比A、B中恰有一个发生的概率大
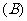 事件A、B同时发生的概率一定比事件A、B恰有一个发生的概率小
事件A、B同时发生的概率一定比事件A、B恰有一个发生的概率小
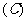 互斥事件一定是对立事件,对立事件不一定是互斥事件
互斥事件一定是对立事件,对立事件不一定是互斥事件
 互斥事件不一定是对立事件,对立事件一定是互斥事件
互斥事件不一定是对立事件,对立事件一定是互斥事件
3.一盒内放有大小相同的10个球,其中有5个红球,3个绿球,2个白球,从中任取2个球,其中至少有1个绿球的概率为 ( )
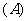
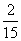
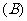
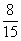
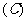
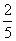
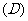
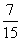
4.在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以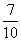 为概率的事件是 ( )
为概率的事件是 ( )
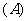 都不是一等品
都不是一等品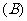 恰有一件一等品
恰有一件一等品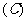 至少有一件一等品
至少有一件一等品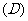 至多一件一等品
至多一件一等品
5.今有光盘驱动器50个,其中一级品45个,二级品5个,从中任取3个,出现二级品的概率为 ( )
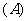
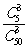
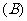
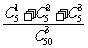
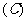 1-
1-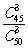
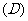
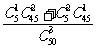
(二)主要方法:
1.弄清互斥事件与对立事件的区别与联系;
2.掌握对立事件与互斥事件的概率公式;
(一)主要知识:
1.互斥事件的概念: ;
2.对立事件的概念: ;
3.若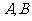 为两个事件,则
为两个事件,则 事件指
.
事件指
.
若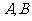 是互斥事件,则
是互斥事件,则 .
.
(四)巩固练习:
1.若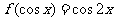 ,
,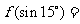 (
(  )
)
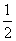
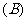
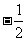
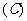
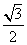
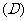
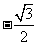
2.已知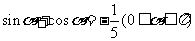 ,则
,则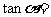
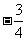 .
.
(三)例题分析:
例1.化简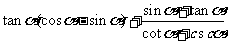
分析:切割化弦是解本题的出发点.
解:原式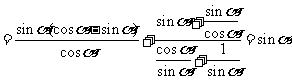 .
.
例2.化简(1)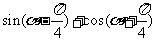 ;
;
(2)已知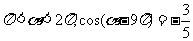 ,求
,求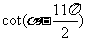 的值.
的值.
解:(1)原式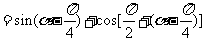
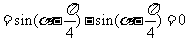 .
.
(2)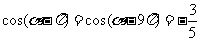 ,∴
,∴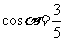 ,
,
∵ ,∴
,∴ ,
,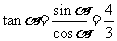 ,
,
∴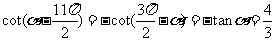 .
.
例3.(1) 若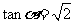 ,求值①
,求值①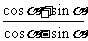 ;②
;②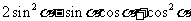 .
.
(2)求值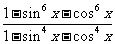 .
.
解:(1)①原式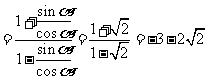 .
.
②∵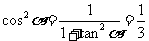 ,
,
∴原式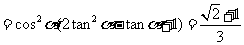 .
.
(2)∵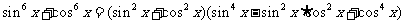
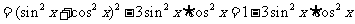 .
.
又∵ .
.
∴原式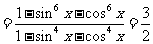 .
.
例4.已知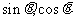 是方程
是方程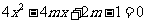 的两个根,
的两个根,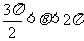 ,求角
,求角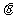 .
.
解:∵ ,代入
,代入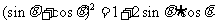 ,
,
得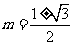 ,又
,又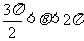 ,∴
,∴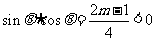 ,
,
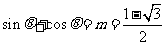 ,∴
,∴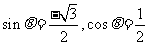 ,又∵
,又∵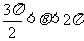 ,
,
∴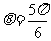 .
.
(二)主要方法:
1.利用同角三角函数的基本关系式时要细心观察题目的特征,注意公式的合理选用,特别要注意开方时的符号选取,切割化弦是常用的方法;
2.学会利用方程的思想解三角题,对于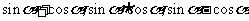 三个式子中,已知其中一个式子的值,可求其余两个式子的值.
三个式子中,已知其中一个式子的值,可求其余两个式子的值.
(一)主要知识:
1.同角三角函数的基本关系式:
(1)倒数关系: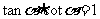 ;
;
(2)商数关系: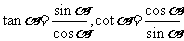 ;
;
(3)平方关系: .
.
2.诱导公式,奇变偶不变,符号看象限.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com