
22、(本题满分12分)
已知函数f(x)=x2-alnx在(1,2]上是增函数,g(x)=x-a 在(0,1)上为减函数;
(Ⅰ)求f(x)、g(x)的表达式;
(Ⅱ)求证:当x>0 时,方程f(x)=g(x)+2有唯一解;
(Ⅲ)当b>-1时,若f(x)≥2bx-对0<x≤1恒成立,求b的取值范围。
21、(本题满分12分)
已知椭圆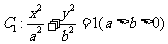 的左、右焦点分别为
的左、右焦点分别为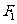 、
、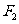 ,其中
,其中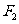 也是抛物线
也是抛物线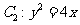 的焦点,
的焦点,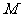 是
是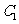 与
与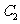 在第一象限的交点,且
在第一象限的交点,且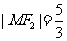 。
。
(Ⅰ)求椭圆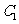 的方程;
的方程;
(Ⅱ)已知菱形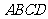 的顶点
的顶点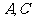 在椭圆
在椭圆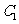 上,对角线
上,对角线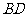 所在的直线的斜率为1.
所在的直线的斜率为1.
① 当直线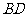 过点
过点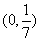 时,求直线
时,求直线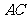 的方程;
的方程;
② 当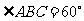 时,求菱形
时,求菱形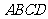 面积的最大值。
面积的最大值。
20、(本小题满分12分)已知函数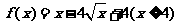 的反函数为
的反函数为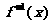 ,数列
,数列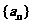 满足:
满足: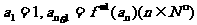 。
。
(Ⅰ)求数列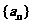 的通项公式;
的通项公式;
(Ⅱ)若数列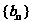 满足:
满足: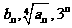 成
成
等比数列,数列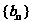 的前n项和为
的前n项和为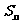 ,求
,求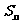 。
。
19、(本小题满分12分)甲、乙两排球队按五局三胜制(先赢三局者最终获胜)进行一次排球比赛,假设在一局比赛中,甲胜乙的概率是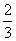 ,各局比赛结果相互独立。
,各局比赛结果相互独立。
(Ⅰ)求乙最终获得这次比赛胜利的概率:
(Ⅱ)设比赛结束时所进行的局数为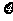 ,求
,求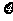 的分布列和数学期望。
的分布列和数学期望。
18、(本小题满分12分)已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1 的中点,M为线段AC1的中点。
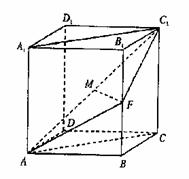 (Ⅰ)求证:直线MF∥平面ABCD;
(Ⅰ)求证:直线MF∥平面ABCD;
(Ⅱ)求证:平面AFC1⊥平面ACC1A1;
(Ⅲ)求平面AFC1与与平面ABCD所成二面角的大小。
17、(本小题满分10分)设函数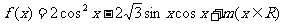 。
。
(Ⅰ)求函数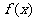 的最小正周期及函数的单调递增区间 ;
的最小正周期及函数的单调递增区间 ;
(Ⅱ)若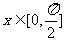 ,是否存在实数m,使函数
,是否存在实数m,使函数 ?若存在,请求出m的取值;若不存在,请说明理由。
?若存在,请求出m的取值;若不存在,请说明理由。
16、已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
①对任意实数k与q,直线l和圆M相切;
②对任意实数k与q,直线l和圆M有公共点;
③对任意实数q,必存在实数k,使得直线l与和圆M相切;
④对任意实数k,必存在实数q,使得直线l与和圆M相切。
其中真命题的代号是______________(写出所有真命题的代号)。
15、设函数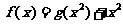 ,曲线
,曲线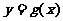 在点(1,
在点(1,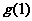 )处的切线方程为
)处的切线方程为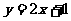 ,则曲线
,则曲线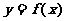 在点
在点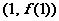 处的切线方程为 。
处的切线方程为 。
14、已知正四面体S-ABC中,点E为SA的中点,点F为△ABC的中心,则异面直线EF、AB所成的角为 。
13、已知随机变量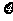 服从正态分布N(
服从正态分布N(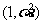 ,且
,且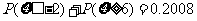 ,则
,则 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com