
4、[解答]设P(x,y),则当∠F1PF2=90°时,点P的轨迹方程为x2+y2=5,由此可得点P的横坐标x=±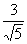 ,又当点P在x轴上时,∠F1PF2=0;点P在y轴上时,∠F1PF2为钝角,由此可得点P横坐标的取值范围是-
,又当点P在x轴上时,∠F1PF2=0;点P在y轴上时,∠F1PF2为钝角,由此可得点P横坐标的取值范围是-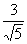 <x<
<x<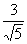 。
。
3、[解答] 由f (x)= -f (x+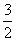 )
) f (x+3)=
f[(x+
f (x+3)=
f[(x+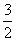 )+
)+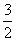 ]=-f (x+
]=-f (x+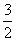 )=f (x)知f (x)是最小正周期T=3的周期函数;由f (x)的图象关于点(
)=f (x)知f (x)是最小正周期T=3的周期函数;由f (x)的图象关于点(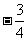 ,0)对称,知(x,y)的对称点是(-
,0)对称,知(x,y)的对称点是(-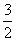 -x,-y).也就是若y=f (x),则必-y=f
(-
-x,-y).也就是若y=f (x),则必-y=f
(-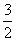 -x),或y=-f (-
-x),或y=-f (-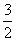 -x). 而已知f (x)=-f (x+
-x). 而已知f (x)=-f (x+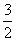 ),故f (-
),故f (-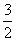 -x)= f
(x+
-x)= f
(x+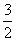 ),今以x代x+
),今以x代x+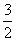 ,得f (-x)=
f (x),故知f (x)又是R上的偶函数.于是有:f (1)=f (-1)=1;f (2)= f (2-3)=f (-1)=1;f (3)= f (0+3)= f (0)=-2;
,得f (-x)=
f (x),故知f (x)又是R上的偶函数.于是有:f (1)=f (-1)=1;f (2)= f (2-3)=f (-1)=1;f (3)= f (0+3)= f (0)=-2;
∴f (1)+f (2)+f (3)=0,以下,这个数列每3项之和为0. 而2009=3×669+2,
于是f (2009)=0×669+f (1)+f (2)=2,故选?A?.
1、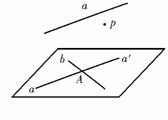 [解答]
[解答]  =
= .这里
.这里 都是负数,故复数
都是负数,故复数 对应的点位于第三象限,选?C?
对应的点位于第三象限,选?C?
2[解答]解:依题若第一道工序由甲来完成,则第四道工序必由丙来完成,故完成方案共有 种;若第一道工序由乙来完成,则第四道工序必由甲、丙二人之一来完成,故完成方案共有
种;若第一道工序由乙来完成,则第四道工序必由甲、丙二人之一来完成,故完成方案共有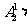
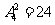 种;∴则不同的安排方案共有
种;∴则不同的安排方案共有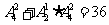 种。
种。
10、将数列{an}的所有项按第1行一个数,第2行2个数,第n行的数的个数是第n – 1行中数的个数的2倍,排成如下数表

记表中第1列的数a1,a2,a4……构成新的数列{bn},b1 = a1 = 1,{bn}前n项的和记为Sn且Sn+1 = 3Sn + 2n+1.
(1)求{bn}的通项公式;
(2)上表中,若从第三行起,每一行中的数从左至右构成等差数列且公差为同一常数,当a260 = 18771时,求上表中第k行(k≥3)中所有数之和Sk
9、已知f (x) = 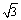 sin
(
sin
(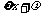 ) –
cos (
) –
cos (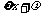 )
(0<
)
(0<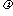 <
<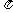 ,
,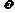 >0),若f (–x) = f (x),f (x)
= f (
>0),若f (–x) = f (x),f (x)
= f (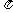 –x)对任意实数x都成立.
–x)对任意实数x都成立.
(i)求f (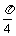 )的值.
)的值.
(ii)将函数y = f (x)的图象向右移 个单位后,再将得到的图象上的各点的横坐标伸长到原来的4倍,纵坐标不变得到函数y = g
(x)的图象,试求y = g (x)的对称中心。
个单位后,再将得到的图象上的各点的横坐标伸长到原来的4倍,纵坐标不变得到函数y = g
(x)的图象,试求y = g (x)的对称中心。
8、某种灯泡的使用时数在1000小时之上的概率是0.7,求:
(1)3个灯泡在使用1000小时之后恰坏1个的概率;
(2)3个灯泡在使用1000小时之后最多只坏1个的概率.
7、 如图,在棱长为a的正方体ABCD-A′B′C′D′中,E、F分别是AB、AC上的动点,满足AE=BF.
如图,在棱长为a的正方体ABCD-A′B′C′D′中,E、F分别是AB、AC上的动点,满足AE=BF.
(Ⅰ)求证: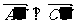 ;
;
(Ⅱ)当三棱锥B′-BEF的体积取得最大值时,
求二面角B′-EF-B的大小(结果用反三角函数表示).
6、如图,非零向量 与
与 轴正半轴的夹角分
轴正半轴的夹角分
别为 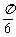 和
和 ,且
,且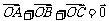 ,则
,则
 与
与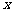 轴正半轴的夹角的取值范围是
轴正半轴的夹角的取值范围是
5、已知m,n是直线,α、β、γ是平面,给出下列是命题:
①若α⊥γ,β⊥γ,则α∥β;②若n⊥α,n⊥β,则α∥β;
③若α内不共线的三点到β的距离都相等,则α∥β;
④若n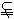 α,m
α,m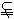 α且n∥β,m∥β,则α∥β;
α且n∥β,m∥β,则α∥β;
⑤若m,n为异面直线,n∈α,n∥β,m∈β,m∥α,则α∥β;
则其中正确的命题是 。(把你认为正确的命题序号都填上)。
4、椭圆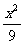 +
+ =1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是
=1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com