
3、定义在R上的函数f (x)的图象关于点(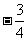 ,0)对称,且满足f (x)= -f (x+
,0)对称,且满足f (x)= -f (x+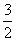 ),f (1)=1,f (0)=-2,则f (1)+f (2)+f (3)+…+f (2009)的值为(
)
),f (1)=1,f (0)=-2,则f (1)+f (2)+f (3)+…+f (2009)的值为(
)
?A.1 B.2 ?C.3 ?D.4
2、生产过程有4道工序,每道工序需要安排一人照看,现从甲乙丙等6名工人
中安排4人分别照看一道工序,第一道工序只能从甲乙两工人中安排1人,第四道工序只能从甲
丙两工人中安排1人,则不同的安排方案有( )
A.24种 B.36种 C.48种 D.72种
1、在复平面内,复数 对应的点位于
( )
对应的点位于
( )
?A.第一 B.第二象限 C.第三象限 D.第四象限
10、[解答](1)由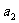 +
+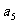 =12,
=12,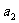
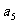 =27,且
=27,且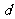 >0,所以
>0,所以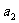 =3,
=3,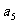 =9,
=9,
从而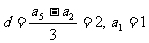 ,
,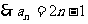
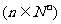
在已知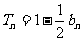 中,令n=1,得
中,令n=1,得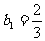
当 时,
时,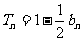 ,
,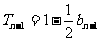 ,两式相减得,
,两式相减得,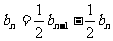 ,
,
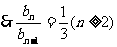 ,
,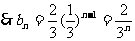

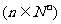
(2)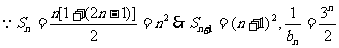
当n=1时,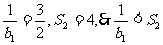 ,当n=2时,
,当n=2时,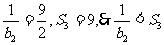 ,
,
当n=3时,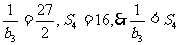 ,当n=4时,
,当n=4时,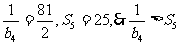 ,
,
猜想: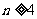 时,
时,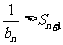 以下用数学归纳法证明:(i)n=4时,已证,
以下用数学归纳法证明:(i)n=4时,已证,
(ii)设n=k(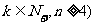 时,
时,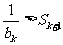 ,即
,即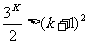 ,则n=k+1时,
,则n=k+1时,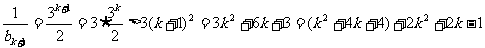
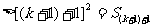 ,
,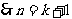 时,
时,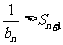 成立
成立 由(i)
由(i) (ii)知
(ii)知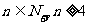 时,
时,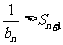
综上所述,当n=1,2,3时,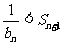 ,当
,当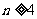 时,
时,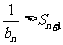

解法二:当n=1,2,3时,同解法一;
当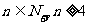 时,
时,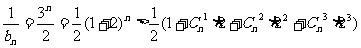
=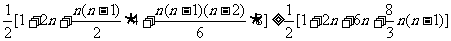
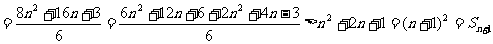 ,
,
综上所述,当n=1,2,3时,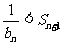 ,当
,当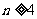 时,
时,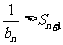
 21世纪教育网
21世纪教育网
9、[解答](Ⅰ)∵()2=·+·+·,∴ ()2=·(+)+· ,
即()2=·+·,即·=0.∴△ABC 是以C为直角顶点的直角三角形.
∴sinA+sinB=sinA+cosA=sin(A+),A∈(0,) ,
∴sinA+sinB的取值范围为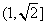 .
.
(Ⅱ)在直角△ABC中, a=csinA,b=ccosA.
若a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a、b、c都成立,
则有≥k,对任意的满足题意的a、b、c都成立,
∵
=[c2sin2A(ccosA+c)+c2cos2A(csinA+c)+c2(csinA+ccosA)]
=[ sin2AcosA+cos2A sinA+1+cosA+sinA]=cosA+sinA+
令t=sinA+cosA,t∈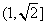 ,
,
设f(t)==t+=t+=t-1++1.
f(t)=t-1++1,当t-1∈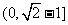 时 f(t)为单调递减函数,
时 f(t)为单调递减函数,
∴当t=时取得最小值,最小值为2+3,即k≤2+3. ∴k的取值范围为(-∞,2+3]
8、[解答] (1)基本事件总数n=C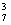 =35, 设事件A={任取3球,至少有一个红球},则事件?
=35, 设事件A={任取3球,至少有一个红球},则事件?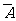 ={任取3球,全是白球}.
={任取3球,全是白球}.
∵A与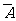 为对立事件,而Card
为对立事件,而Card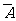 =1(任取3球全是白球仅一种可能).
=1(任取3球全是白球仅一种可能).
∴P(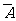 )=
)=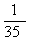 ,于是P (A)=1-P (
,于是P (A)=1-P (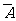 )=
)=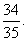 即该顾客任取3球,至少有一个红球的概率为
即该顾客任取3球,至少有一个红球的概率为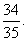
(2)ξ=50表示所取4球为3白1红(∵3×10+1×20=50),∴P (ξ=50)=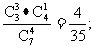
ξ=60表示所取4球为2白2红(∵2×10+2×20=60), ∴P (ξ=60)= 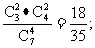 ?
?
ξ=70表示所取4球为3红1白(∵3×20+1×10=70), ∴P (ξ=70)= 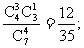
ξ=80表示所取4球全为红球, ∴P (ξ=80)= 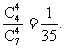
于是ξ的分布列为:
|
ξ |
50 |
60 |
70 |
80 |
|
P |
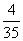 |
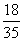 |
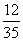 |
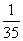 |
∴Dξ=50×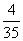 +60×
+60×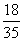 +70×
+70×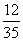 +80×
+80×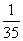 =
=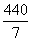 (元).即该顾客获奖的期望是
(元).即该顾客获奖的期望是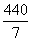 ≈63(元).
≈63(元).
7、分析 (1)为证PD⊥PC,须先证PD⊥平面PBC,已有PD⊥PB(翻折前为AD⊥AB),还须PD⊥BC.
(2)求二面角的要点是找出二面角的平面角,已有PO⊥平面BCD于O,且?O∈CD?,只须作OM⊥BD?即可.?
[解答] (1)由条件知PO⊥平面BCD于O,且?O∈CD,?BC⊥CD,∴BC⊥PD(三垂线定理),但PD⊥PB,∴PD⊥面PBC,从而PD⊥PC.
(2)作OM⊥BD于M,连接PM,则BD⊥PM(三垂线定理),∴∠PMO是二面角P-BD-C的平面角,
∵PB=6, PD=2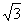 ,∴BD=4
,∴BD=4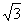 ,PM=
,PM=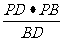 =3,
=3,
已证PD⊥PC,∴PC=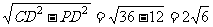 ,PO=
,PO=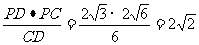 .
.
?sin∠PMO=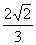 ,∠PMO=arcsin
,∠PMO=arcsin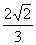 ,即所求二面角P-DB-C的大小为?arcsin
,即所求二面角P-DB-C的大小为?arcsin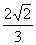 .
.
6、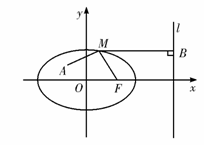 [解答]注意到椭圆的离心率
[解答]注意到椭圆的离心率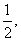 与结论中线段|MF|的系数之间的数量关系,
与结论中线段|MF|的系数之间的数量关系,
作MB垂直于右准线l,垂足为B,如图所示.则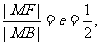
即|MB|=2|MF|, 所以|MA|+2|MF|=|MA|+|MB|.
易知点M在线段AB上时,|MA|+2|MF|取最小值8,这时点M的坐标 为(2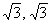 ).
).
5、[解答]设函数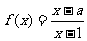 , 集合
, 集合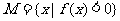 .
.
若a>1时,M={x| 1<x<a};
若a<1时,M={x| a<x<1};
若a=1时,M=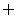 .
.
 ,∴
,∴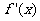 =
=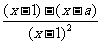 >0.
>0.
∴ a>1时,P=R,a<1时,P= ;已知
;已知 ,所以 (1,+∞).
,所以 (1,+∞).
4、[解答]如图所示,令A1P = CQ = 0. 即动点P与A1重合,动点Q与C重合.
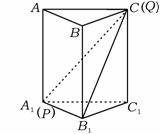 则多面体蜕变为四棱锥C-AA1B1B,四棱锥蜕化为三棱锥C-A1B1C1 .
则多面体蜕变为四棱锥C-AA1B1B,四棱锥蜕化为三棱锥C-A1B1C1 .
显然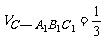 V棱柱.∴
V棱柱.∴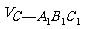 ∶
∶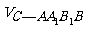 =
=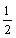
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com