
3.
例3设PQ是过抛物线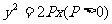 焦点F的一条弦,若P(
焦点F的一条弦,若P(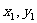 ),Q(
),Q( )且PQ的倾斜角为
)且PQ的倾斜角为
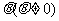 则有以下结论:①
则有以下结论:①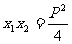 ,
,  ②
② ③
③ ④
④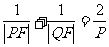

冲刺强化训练(14)
2.
例2用待定系数法求双曲线的标准方程,一定要抓住题设所给的独立条件建立 之间的等量关系,再利用
之间的等量关系,再利用 运用方程的思想来求解。
运用方程的思想来求解。
1. 例1运用了椭圆的两种定义来解决,椭圆两定义都是椭圆上任意一点P到焦点的距离来描述的,这两种定义能够对一些距离进行相关的转化、简化解题过程。因此在解答时遇到涉及曲线上点到焦点的距离时应该考虑是否能够使用椭圆的定义求解。
例1.已知A、B是椭圆 上的点,
上的点,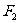 是右焦点且
是右焦点且 ,AB的中点N到左准线的距离等于
,AB的中点N到左准线的距离等于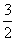 ,求此椭圆的方程。
,求此椭圆的方程。


例2.已知双曲线 (
( )的右准线
)的右准线 与一条渐近线
与一条渐近线 交于点P,F是双曲线的右焦点:
交于点P,F是双曲线的右焦点:
(1)求证: ;
;
(2)若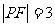 且双曲线的离心率
且双曲线的离心率 ,求双曲线的方程;
,求双曲线的方程;
(3)延长FP交双曲线左准线 和左支分别为M、N,若M为PN的中点,求双曲线的离心率
和左支分别为M、N,若M为PN的中点,求双曲线的离心率





例3(选讲).抛物线有光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出。今有抛物线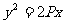 (
(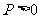 ),一光源在点M(
),一光源在点M(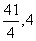 )处,由其发出的光线沿平行于抛物线的对称轴方向射向抛物线上的点P,反射后又射向抛物线上的点Q,再反射后又沿平行于抛物线的对称轴的方向射出,途中遇到直线
)处,由其发出的光线沿平行于抛物线的对称轴方向射向抛物线上的点P,反射后又射向抛物线上的点Q,再反射后又沿平行于抛物线的对称轴的方向射出,途中遇到直线 :
: 上的点N,再反射后又射回到点M
上的点N,再反射后又射回到点M
(1)
设P、Q两点的坐标分别为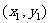 ,
, ,证明:
,证明: ;
;
(2)
求抛物线的方程;
(3)
试判断在抛物线上是否存在一点R使该点与点M关于PN所在直线对称?若存在请求出此点的坐标;若不存在,请说明理由。



|
|
|
|
|
|
|







5.点A的坐标为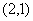 ,F为抛物线
,F为抛物线 的焦点,P在抛物线上移动,若
的焦点,P在抛物线上移动,若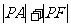 取最小值,则点P的坐标为
取最小值,则点P的坐标为

4.已知双曲线中心在原点且一个焦点为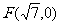 ,直线
,直线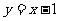 与其相交于M、N两点MN的中点的横坐标为
与其相交于M、N两点MN的中点的横坐标为 ,则此双曲线方程是
,则此双曲线方程是

3.动点P在椭圆 上运动,线段OP长度的最大值是( )
上运动,线段OP长度的最大值是( )
(A)1 (B)2
(C)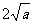 (D)
(D)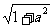

2.以椭圆 的中心为焦点,右准线为准线的抛物线与椭圆的左准线交于A、B两点,则
的中心为焦点,右准线为准线的抛物线与椭圆的左准线交于A、B两点,则 的值是( )
的值是( )
(A)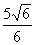 (B)
(B) (C)
(C) (D)
(D)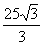

1.若 ,则方程
,则方程 所表示的曲线必定不是( )
所表示的曲线必定不是( )
(A)直线
(B)圆
(C)双曲线
(D)抛物线
3、理解圆和椭圆的参数方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com