
2、黄河流域治理措施:
1、黄土高原水土流失原因分析:
21.解 :(1)由点P
:(1)由点P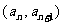 在直线
在直线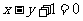 上,即
上,即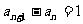 , …………2分
, …………2分
且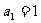 ,数列{
,数列{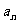 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列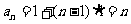 ,
,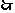
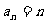 ……………4分
……………4分
(2)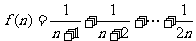
 …………………6分
…………………6分

所以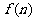 是单调递增,故
是单调递增,故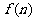 的最小值是
的最小值是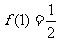 ……………10分
……………10分
 (3)
(3)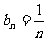 ,可得
,可得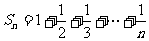 ,
, ……………11分
……………11分
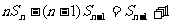 ……………12分
……………12分
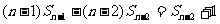
…………
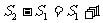



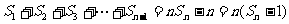 ,
,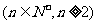 ……………14分
……………14分
另解:
此式中有 个1,有
个1,有 个
个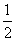 ,
, ,1个
,1个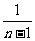 。
………………12分
。
………………12分

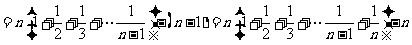


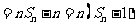 。
。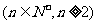 ………………14分
………………14分
20.解:(1)由题意得|PA|=|PB|且|PB|+|PF|=r=8. 故|PA|+|PF|=8>|AF|=4
∴P点轨迹为以A、F为焦点的椭圆.………………………………………………… 3分
设椭圆方程为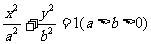
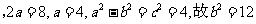
 . …………………………………………………… 6分
. …………………………………………………… 6分
(2)假设存在满足题意的直线L.易知当直线的斜率不存在时, 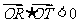 不满足题意.
不满足题意.
故设直线L的斜率为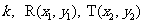 .
.
 ………………………………………………7分
………………………………………………7分
 ……………………………………8分
……………………………………8分
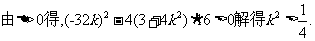 ……………………①.
……………………①.
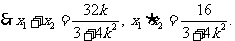 ……………………………………………10分
……………………………………………10分
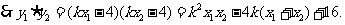 ………………………11分
………………………11分

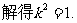 …②.
…②.
由①、②解得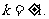
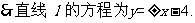 ……………………………………………………13分
……………………………………………………13分
 ……………………14分
……………………14分
19.解:(1)直线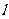 是函数
是函数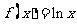 在点
在点 处的切线,故其斜率
处的切线,故其斜率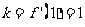 ,
,
∴直线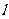 的方程为
的方程为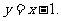 …………………2分
…………………2分
又因为直线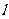 与
与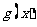 的图象相切,且切于点
的图象相切,且切于点 ,
,
∴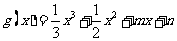 在点
在点 的导函数值为1.
的导函数值为1.
 ,∴
,∴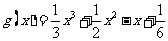 …………………6分
…………………6分
(2)
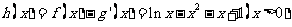 …………………7分
…………………7分
∴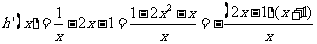 …………………9分
…………………9分
当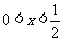 时,
时,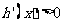 ;当
;当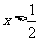 时,
时,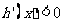 …………………11分
…………………11分
因此,当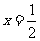 时,
时,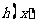 取得极大值,
取得极大值, 

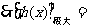
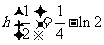 …………………14分
…………………14分
18.证明: (1) 连接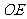 ,
,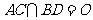 ,
, 

在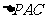 中,∵
中,∵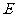 为PC的中点,
为PC的中点,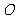 为
为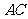 中点.
中点.

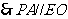 , ………………3分
, ………………3分
又∵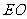
 平面
平面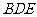 ,
,
 平面
平面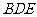 ,
,
∴ //平面
//平面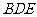 ………………6分
………………6分
(2)∵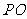
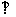 底面
底面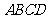 ,
,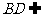 底面
底面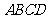 ,
,
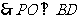 。
……………… 9分
。
……………… 9分
又∵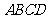 是正方形,
是正方形,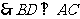 ,
,
又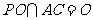 ,∴
,∴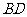
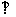 平面
平面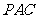 .
.
又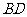
 平面
平面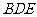 ,
,
∴平面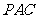
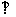 平面
平面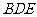 . ……………12分
. ……………12分
17.解:(1)分别从集合A,B中各取一个数组成数对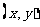 ,共有25对,……………2分
,共有25对,……………2分
其中满足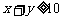 的有
的有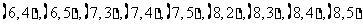 ,共9对
…………………………5分
,共9对
…………………………5分
故使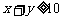 的概率为:
的概率为: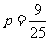 .
…………………………7分
.
…………………………7分
(2)用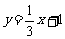 作为拟合直线时,所得
作为拟合直线时,所得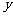 的实际值与
的实际值与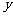 的估计值的差的平方和为:
的估计值的差的平方和为:
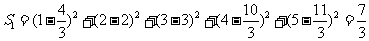 . ………………10分
. ………………10分
用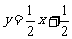 作为拟合直线时,所得
作为拟合直线时,所得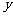 的实际值与
的实际值与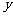 的估计值的差的平方和为:
的估计值的差的平方和为:
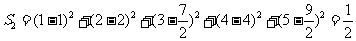 . ………………12分
. ………………12分
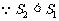 ,故用直线
,故用直线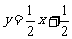 拟合程度更好. ………………14分
拟合程度更好. ………………14分
16.解:(1)由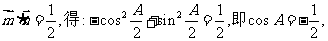 …………………4分
…………………4分
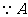 为
为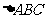 的内角,
的内角,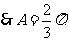 …………………………………6分
…………………………………6分
(2)由余弦定理: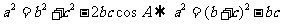
即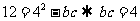 ………………………………………………………10分
………………………………………………………10分
又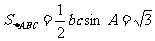 . …………………………………………………12分
. …………………………………………………12分
15.解:连接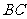 ,
,
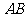 是
是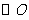 的直径
的直径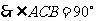 ,
,
又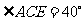 ,
,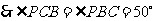 ,
,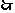
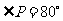
14.解:极点的直角坐标为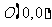 ,
,
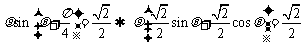
 ,化为直角坐标方程为:
,化为直角坐标方程为: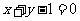 ;
;
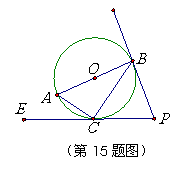
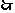 点
点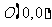 到直线
到直线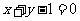 的距离为
的距离为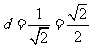 。
。
即极点到直线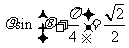 的距离为
的距离为 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com