
1.已知p: ≤2,q:x2―2x+1―m2≤0(m>0)
≤2,q:x2―2x+1―m2≤0(m>0)
又知非p是非q的必要条件,但不是充分条件,求取m的取值范围.
5.已知a、b、c为非零平面向量。甲:a·b=a·c,乙:b=c, 则 ( )
(A)甲是乙的充分条件但不是必要条件 (B)甲是乙的必要条件但不是充分条件
(C)甲是乙的充要条件 (D) 甲既不是乙的充分条件也不是乙的必要条件。
4.设命题p:∣4x-3∣≤1;命题q: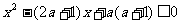 。若非p是非q的必要而不充分条件,则实数a的取值范围是
。
。若非p是非q的必要而不充分条件,则实数a的取值范围是
。
3.直线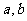 和平面
和平面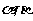 ,
,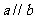 的一个充分条件是(
)
的一个充分条件是(
)
A. B.
B.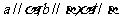
C. 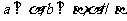 D.
D.
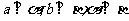
2.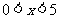 是
是 的
条件.
的
条件.
1.若非空集合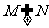 ,则“
,则“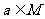 或
或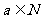 ”是“
”是“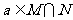 ”的
条件.
”的
条件.
考题1 (2002全国)函数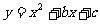 在
在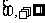 是增函数的充要条件是 ( )
是增函数的充要条件是 ( )
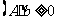
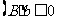


考题2(2000上海)“ ”是“函数
”是“函数 的最小正周期为
的最小正周期为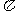 ”的(
)
”的(
)
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)即不充分又不必要条件
考题3(2006安徽)设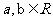 ,已知命题
,已知命题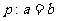 ;命题
;命题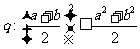 ,则
,则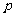 是
是 成立的
( )
成立的
( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
考题4(2006湖南文)“a=1”是“函数 在区间[1,+∞)上为增函数”的
在区间[1,+∞)上为增函数”的
A.充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
考题5(2006江西文)下列四个条件中,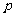 是
是 的必要不充分条件的是 ( )
的必要不充分条件的是 ( )
A. ,
,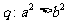 B.
B. ,
,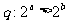
C.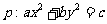 为双曲线,
为双曲线,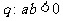 D.
D.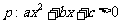 ,
,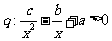
考题6(2006山东)设p:x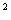 -x-20>0,q:
-x-20>0,q: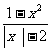 <0,则p是q的
<0,则p是q的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
考题7(2004福建)命题p:若 a、b∈R,则∣a∣+∣b∣>1是∣a+b∣>1的充分而不必要条件;命题q:函数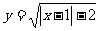 的定义域是
的定义域是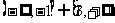 ,则( )
,则( )
(A)“p或q”为假 (B)“p且q”为真 (C) p真q假 (D) p假q真
例1.指出下列各组命题中, 是
是 的什么条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选一种作答)
的什么条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选一种作答)
(1)在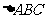 中,
中,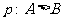 ,
,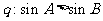
(2)对于实数 ,
,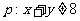 ,
,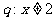 或
或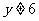
(3)在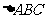 中,
中,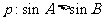 ,
,
(4)已知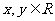 ,
, ,
,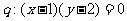
例2.设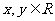 ,则
,则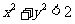 是
是 的(
)、是
的(
)、是 的(
)
的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
例3.若命题甲是命题乙的充分非必要条件,命题丙是命题乙的必要非充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
例4.设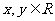 ,求证:
,求证: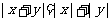 成立的充要条件是
成立的充要条件是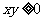 .
.
例5.已知数列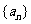 的通项
的通项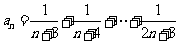 ,为了使不等式
,为了使不等式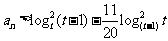 对任意
对任意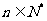 恒成立的充要条件.
恒成立的充要条件.
例6.(1)是否存在实数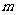 ,使得
,使得 是
是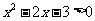 的充分条件?
的充分条件?
(2)是否存在实数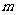 ,使得
,使得 是
是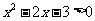 的必要条件?
的必要条件?
4.探索充要条件:在探索一个结论成立的充要条件时,一般先探索必要条件,再确定充分条件;也可以一些基本的等价关系来探索。
3.判断充要条件关系的三种方法:
①定义法:若 ,
, 则A是B的充分条件,B是A的必要条件;
则A是B的充分条件,B是A的必要条件;
若 ,则A是B的充要条件。
,则A是B的充要条件。
②利用原命题和逆否命题的等价性来确定 “若A,则B”及“若B,则A”的真假性。
③利用集合的包含关系:若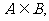
 则A是B的充分条件,B是A的必要条件;
则A是B的充分条件,B是A的必要条件;
若A=B,则A是B的充要条件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com