2、过程和方法目标：通过生活中实际问题的引入来创设情境，激发学生学习的兴趣。经过小

组讨论后可以将一些生活问题构建成一个等可能性事件模型，学生的构建思维能力得到提升。

在归纳定义时运用由特殊到一般的思想；在解题时运用类比的方法，举一反三。通过枚举法、

数状图法、图表法、排列组合等方法来计算一些等可能性事件的概率，学生对古典概型有个

更深刻的理解。

1、知识与技能目标：了解等可能性事件的概率的意义，运用枚举法计算一些等可能性事件的

概率。

3、古典概型的地位和作用

古典概型在概率论中占有重要的地位。其意义在于：

(1)有利于理解概率的概念，当研究这种概型时，频率的稳定性容易得到验证，从而概率的稳定值与理论上算出的概率值的一致性容易得到验证，从而概率值的存在性易于被学生理解。

(2)有利于计算事件的概率。在古典概型范围内研究问题，避免了进行重复试验。

(3)这种概型的实际应用较广，因而学习这种概型有助于运用所学知识解决某些实际问题。

2、概念解析

(1)核心内容: 概括等可能性事件的概率的概念和构建等可能性事件模型。

(2)思想方法：特殊到一般的方法--通过举特例概括等可能性事件和等可能性事件概率的概念；类比的思想方法--类比抛掷一个均匀骰子两次到抛掷一个骰子三次；对称的数学思想--通过图表观察出对称的规律。

1、概念

(1)基本事件：一次试验连同其中可能出现的每一个结果称为一个基本事件。

(2)等可能性事件：如果一次试验由n个基本事件组成，而且所有的基本事件出现的可能性都相等，那么这个事件叫做等可能性事件。

(3)等可能事件性的概率：如果一次试验中可能出现的结果有n个，而且所有结果出现的可能性相等，那么每一个基本事件的概率都是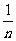,如果某个事件包含的结果有m个，那么事件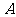的概率：。

2、思考题：以小组为单位为桂林微笑堂设计一个十一国庆商场促销的摸奖活动方案。

“等可能性事件的概率”教学说明

1、P₁₄₁　 习题11.1　 2，3，5

9、课后作业：

3、求等可能性事件概率的步骤：

(1)审清题意，判断本试验是否为等可能性事件。

(2)计算所有基本事件的总结果数n。

(3)计算事件A所包含的结果数m。

(4)计算P(A)=m/n。

(老师)其实，概率论与生活是紧密联系的，学好它可以更好的为生活服务，因为概率论在天气的预测，保险行业，信息学等方面都有很大的用途。希望同学们学好概率。

2、等可能性事件的特征：

(1)、一次试验中有可能出现的结果是有限的。

(2)、每一结果出现的可能性相等。