
考题1 (2005山东)函数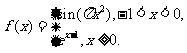 ,若
,若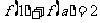 则
则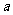 的所有可
的所有可
能值为( )
(
A)1
(B)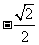 (C)
(C)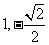 (D)
(D)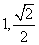
考题2(2005浙江)设f(x)=|x-1|-|x|,则f[f(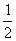 )]=
( )
)]=
( )
(A)
-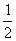 (B)0
(C)
(B)0
(C)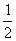 (D)
1
(D)
1
考题3(2005江苏)若函数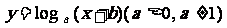 的图象过两点
的图象过两点
(-1,0)和(0,1),则 ( )
(A)a=2,b=2 (B)a=,b=2 (C)a=2,b=1 (D)a=,b=
考题4(2006辽宁文)设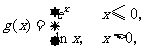 则
则
考题5(2006安徽)函数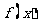 对于任意实数
对于任意实数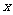 满足条件
满足条件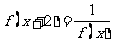 ,若
,若 则
则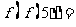 _______________。
_______________。
考题6(2003全国)已知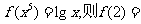 ( )
( )
(A)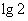 (B)
(B)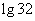 (C)
(C)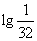 (D)
(D)
例1.(1)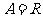 ,
,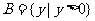 ,
, ;
;
(2)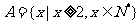 ,
,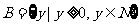 ,
,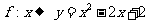 ;
;
(3)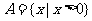 ,
,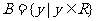 ,
,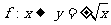 .
.
上述三个对应
是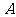 到
到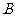 的映射.
的映射.
例2.已知集合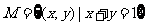 ,映射
,映射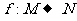 ,在
,在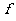 作用下点
作用下点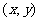 的象是
的象是 ,则集合
,则集合 ( )
( )
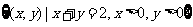
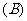
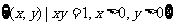
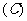
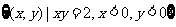
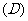
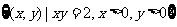
例3.设集合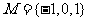 ,
,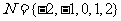 ,如果从
,如果从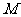 到
到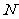 的映射
的映射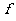 满足条件:对
满足条件:对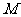 中的每个元素
中的每个元素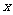 与它在
与它在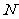 中的象
中的象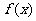 的和都为奇数,则映射
的和都为奇数,则映射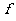 的个数是 ( )
的个数是 ( )
 8个
8个
 12个
12个
 16个
16个
 18个
18个
例4
设函数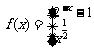
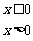 ,若
,若 ,则
,则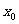 的取值范围是 ( )
的取值范围是 ( )
(A)(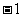 ,1)
(B)(
,1)
(B)(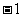 ,
, )
)
(C)( ,
,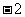 )
)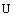 (0,
(0, )
(D)(
)
(D)( ,
,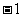 )
) (1,
(1, )
)
例5.矩形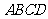 的长
的长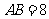 ,宽
,宽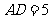 ,动点
,动点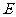 、
、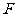 分别在
分别在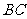 、
、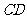 上,且
上,且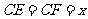 ,(1)将
,(1)将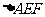 的面积
的面积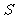 表示为
表示为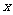 的函数
的函数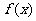 ,求函数
,求函数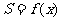 的解析式;
的解析式;
(2)求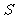 的最大值.
的最大值.
3.理解函数和映射的关系,函数式和方程式的关系.
2.对函数三要素及其之间的关系给以深刻理解,这是处理函数问题的关键;
1.对映射有两个关键点:一是有象,二是象惟一,缺一不可;
3.正确理解函数值的含义,掌握函数值的求法,会灵活解决有关函数值的问题;特别是涉及分段函数或复合函数的值的问题.
2.函数的三要素及表示法,两个函数相同的条件;
1.映射与函数的概念;
7.已知关于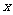 的方程
的方程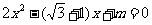 的两根为
的两根为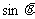 和
和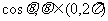 ,
,
(1)求实数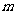 的值;
的值;
(2)求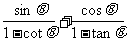 的值;(其中
的值;(其中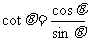 )
)
6.函数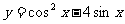 的值域是
。
的值域是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com