3、等比数列的通项公式

我们继续来研究一下情境中的这三个数列。

探究3：试着写出上面三个数列的通项公式，并猜想等比数列的通项公式。

[设计意图]体现由特殊到一般的思想，先写出具体实例的通项公式，使学生经历观察，归纳，猜想的过程。

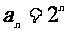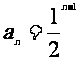①　 　②　　　 ③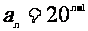

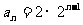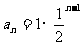[学生]通过观察，看出这三个数列的通项公式，并寻找这三个公式中共性的地方，把①改写成，②，③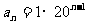，观察，发现都有n-1次幂的形式，而且乘号前面的数字2,1,1都是首项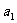，乘号后面的数字2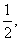，20都是各项的公比，所以猜想等比数列的通项公式是a_n=a₁q^n-1。

[老师]这位同学猜想的很好，那我们就来推导一下等比数列的通项公式，看看和这位同学猜想的一致吗？

探究4： 类比等差数列通项公式的推导过程，请你写出首项为a1，公比是q的等比数列的通项公式。

[老师]我们在学习等差数列的通项公式时，用过哪些方法？

[学生1]回忆了用不完全归纳法证明通项公式的方法，类比等差数列的推导过程，设等比数列{a_n}首项为a₁，公比为q，根据等比数列的定义，我们有：

a₂=a₁q,

a₃=a₂q=a₁q²,…

即a_n=a₁q^n-1.

[老师]请同学们想一想，你还有其它方法吗？

[学生2]根据等比数列的定义，我们还可以写出

,

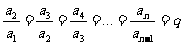进而有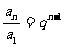，即a_n=a₁q^n-1.

[学生3]a_n=a_n-1q=a _n-2q²=a _n-3q³=…=a₁q ^n-1.亦得a_n=a₁q^n-1。

[老师]等比数列的通项公式：a_n=a₁q^n-1 　(n∈N﹡,q≠0)

我们知道了等比数列的通项公式后，下面我们做课本52页练习，来看一下它有哪些应用。

学生做练习，老师巡视，予以指导。

探究5：在课本50页的平面直角坐标系中，

　(1)画出通项公式为a_n=2 ^n-1的数列的图象。

　(2)再在坐标系中画出函数y=2^x-1的图象，观察它们之间的关系。

(3)若将底数换为 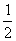　呢？你有怎样的结论？

[设计意图]等比数列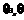的通项公式还可以写成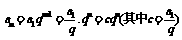，当q为不等于1的正数时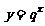，是一个指数函数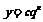，是一个的非零常数与一个指数函数的积。因此从图像上看，表示数列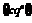的点都在函数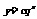的图像上。

[学生]观察、动手作图，发现规律，总结规律，数列是特殊的函数，等比数列是其对应函数图象上孤立的点。

[老师]通过几何画板演示动画。

2、等比中项

探究2：前面的等差数列一节里我们有等差中项的定义，你能仿照等差中项，给出等比中项的定义吗？等差中项与等比中项有何差异？

[老师]类比等差中项的概念，大家给等比中项下个定义吧。

[学生]如果在a与b中间插入一个数G，使a，G，b成等比数列，那么G叫做a与b的等比中项。学生思考得结论：任何两个数都有等差中项，有且只有一个，而只有同号的两个数才有等比中项，而且有两个，且互为相反数。

在前几节课中,我们学习了等差数列的定义、等差数列的通项公式及等差中项的定义，今天我们就来学习另外一种特殊的数列，首先看实例1。

l　　　 实例分析1：在《数学3》(必修)中，我们认识了二进制数。它是一串由“0”和“1”构成的数。计算机存储数据时就是以二进制数的形式储存的。计算机存储的最基本单位是“位(bit)”，每一位只能存储一个“0”或一个“1”，所以1个位可以存储0、1两种不同的信息.如果有2个位，就可以存储00、01、10、11四种不同的信息.我们记n个位共能储存的不同信息 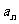　种，写出{　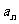 　}的前5项。

[老师]首先请一位同学读题，最后一句话说的是什么含义呢？老师引导学生分析本题的含义，并画出树状图形象的表示。

[学生]通过观察，分析，理解题意，从而得到{　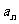 　}的前5项为2,4,8,16,32。　　 ①

l　　　　 实例分析2：公元前5至前3世纪，中国战国时，《庄子》一书中有“一尺之棰，日取其半，万世不竭”的关于物质无限可分的观点。你能解释这个论述的含义吗？

[学生]思考、讨论，用现代语言叙述。

[老师] (用现代语言叙述后)如果把“一尺之棰”看成单位“1”，那么得到的数列是什么样的呢？

[学生]发现等比关系，写出一个无穷等比数列：1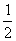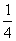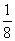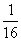，，，，，…。　②

[老师]大家知道计算机病毒的传播是非常快的，速度大的惊人，那么让我们看一个这样的实例。

l　　　　 实例分析3：一种计算机病毒可以查找计算机中的地址薄，通过邮件进行传播。如果把病毒制造者发送病毒称为第一轮，邮件接收者发送病毒称为第二轮，依此类推。假设每一轮每一台计算机都感染20台计算机，那么在不重复的情况下，这种病毒每一轮感染的计算机数构成的数列是什么？

[学生]合作讨论,得出什么为第一轮，第二轮。从而得到种病毒每一轮感染的计算机数构成的数列是1,20,20²，20³,…。③

[老师]回忆数列的等差关系和等差数列的定义，观察上面的数列①②③，说说它们有什么共同特点？引导学生类比等差关系和等差数列的概念，发现等比关系。我们可以发现：

数列①从第2项起,每一项与它前一项的比都等于____；

数列②从第2项起,每一项与它前一项的比都等于____；

数列③从第2项起,每一项与它前一项的比都等于____；

也就是说这个数列有一个共同的特点：从第2项起,每一项与它前一项的比等于同一个常数。

我们把这样的数列称为等比数列。这就是我们今天要研究的课题，等比数列。

[设计意图]目的是让学生明白等比数列是来源于生活中的例子，观察所给各个数列的共同特点，进一步归纳出等比数列的定义。

在本节课的教学中，我采用了如下的教学方法：问题式教学法、 启发式教学法、 三动式教学法。

(1)问题式教学法

整个教学过程以“问题串”的形式贯穿始终，使学生一环扣一环，在有效问题的驱动下进行积极地思考，探究，类比，讨论，学习知识。

(2)发现式教学法：

新课程倡导：强调过程，强调学生探索新知识的经历和获得新知的体验，不能再让教学脱离学生的内心感受，必须让学生有追求过程的体验．在教学中，给提供学生自主探索的空间和余地，让学生充分体验数学知识的形成过程，让学生经历观察、分析、猜想、抽象、概括、归纳、类比等发现和探索的过程，把人类已发现的“现成的数学”在教师的指导下变为学生亲自“发现”的结论，也就是学生自己“做出来的数学”。这种亲身体验和经历的过程，如同是重新经历数学的发现过程，也就是学生的“再发现”过程，可以启迪学生发现问题，再创造的解决问题，为以后适应社会发展，解决面临的新问题、新情况做好基础的铺垫。

(3)三动式教学法

　　 这个三动式教学法具体是指师生互动、生生互动、落实行动。在整个教学过程中，始终坚持这三方面，充分发挥教师为主导，学生为主体的地位，充分的把时间留给学生，并注重学完每个小知识点后的及时的练习，落实行动。

(4)类比探究式学习法

教学中遵循“学生为主体，教师为主导，知识为主线，发展思维为主旨”的“四主”原则．以恰当的问题为纽带，给学生创设自主探究、合作交流的空间，指导学生类比探究形成概念．引导学生经历数学知识再发现的过程，让学生在参与中获取知识，发展思维，感悟数学。

总之，这节课最大的特点是处处站在学生的立场上去对待问题的发现和处理，整节课流畅又不失起伏，学生的参与意识被充分地调动起来，使得整节课激情四射、高潮迭起、精彩纷呈；同时注意对重、难点知识采用“欲扬先抑”的方法，让学生在探索、类比中发现，精心设计的问题巧妙地串起每个知识点，使得整节课有一气呵成之感！

3、学生在做探究5探究等比数列的图象与函数的关系时，会作出等比数列的图象，可能在得到和具体函数图象的关系时存在困难，因此通过学生亲自动手作图，老师几何画板演示，讨论，展示，从而突破难点。

2、学生在做练习2(1)的时候，只得到一个值3，而少了-3。正因为这点，我们更需要学习等比中项的定义，掌握它的内涵。

练习2：求下列各组数中插入怎样的数后是等比数列。

(1)1， ____ ，　 9　　

　本节课学生很容易在以下三个地方产生错误或困惑：

1、　 在等比数列的定义中漏掉q≠0的条件。

学生在类比等差数列的定义去自主探究等比数列的定义的时候，发现自己定义的等比数列的概念和书上对比，缺少了q≠0的这个条件，然后思考为什么课本中有这个条件，没有行不行。通过学生自己探究发现问题，解决问题，从而突出重点。

3、 通过等比数列与指数函数的关系体会数列是一种特殊的函数。

目标解析：

教学目标(1)和(2)是重点内容，教学目标(3)是难点内容。通过从丰富实例中抽象出的等比数列模型，使学生认识到这一类数列也是现实世界中大量存在的数列模型；同时经历由发现几个具体数列的等比关系，归纳出等比数列的定义的过程。通过与等差数列通项公式的推导过程类比，探索等比数列的通项公式；通过与指数函数的图像类比，探索等比数列的通项公式的图像特征与指数函数之间的联系。

2、　 探索并掌握等比数列的通项公式

通过等差数列的通项公式的推导过程的类比，探索等比数列的通项公式，通过与指数函数的图象类比，探索等比数列的通项公式的图象特征及与指数函数之间的关系。