
4、(湖北省黄冈市2007年秋季高三年级期末考试)在平面直角坐标系中,O为坐标原点,已知向量 ,又点
,又点
(1)若 且
且 ,求向量
,求向量 ;
;
(2)若向量 与向量
与向量 共线,当
共线,当 时,且
时,且 取最大值为4时,求
取最大值为4时,求
解: 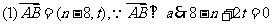
又 ,得
,得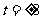 (4分)
(4分)
 或
或

 与
与 向量共线,
向量共线, 
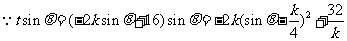
 ,
, 当
当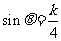 时,
时, 取最大值为
取最大值为 (8分)
(8分)
由 ,得
,得 ,此时
,此时
 (12分)
(12分)
3、(山东省博兴二中高三第三次月考)已知 ,其中
,其中 。
。
(1)求证: 与
与 互相垂直;
互相垂直;
(2)若 与
与 (
( )的长度相等,求
)的长度相等,求 。
。
解析:(1)因为

所以 与
与 互相垂直。
互相垂直。
(2) ,
,
 ,
,
所以 ,
,
 ,
,
因为 ,
,
所以 ,
,
有 ,
,
因为 ,故
,故 ,
,
又因为 ,
,
所以 。
。
2、(北京市丰台区2008年4月高三统一练习一)已知 ,
, 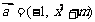 ,
, ,
, .
.
(Ⅰ)当 时,求使不等式
时,求使不等式 成立的x的取值范围;
成立的x的取值范围;
(Ⅱ)求使不等式 成立的x的取值范围.
成立的x的取值范围.
解:(Ⅰ)当 时,
时,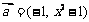 ,
, .
.

 .
……………………………………… 2分
.
……………………………………… 2分
∵  ,
,
∴  解得
解得
 或
或 .
.
∴ 当 时,使不等式
时,使不等式 成立的x的取值范围是
成立的x的取值范围是
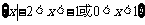 .…………………………………………… 5分
.…………………………………………… 5分
(Ⅱ)∵  ,…… 8分
,…… 8分
∴ 当m<0时, ;
;
当m=0时,  ;
;
当 时,
时,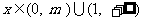 ;
;
当m=1时, ;
;
当m>1时, .
.
1、(四川省巴蜀联盟2008届高三年级第二次联考)设向量
 ,其中
,其中 .
.
(1)求 的取值范围;
的取值范围;
(2)若函数 的大小
的大小
解:(1)∵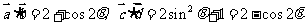 ,∴
,∴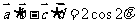 ,
,
∵ ,∴
,∴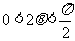 ,∴
,∴ ,
,
∴ 。
。
(2)∵ ,
,
 ,
,
∴ ,
,
∵ ,∴
,∴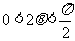 ,∴
,∴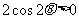 ,∴
,∴
30、
29、(山西省实验中学2007-2008学年度高三年级第四次月考)已知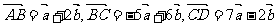 ,则点A、B、C、D中一定共线的三点是
。
,则点A、B、C、D中一定共线的三点是
。
答案:A、B、D
28、(山东省聊城市2008届第一期末统考)定义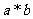 是向量a和b的“向量积”,它的长度
是向量a和b的“向量积”,它的长度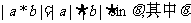 为向量a和b的夹角,若
为向量a和b的夹角,若 =
.
=
.
答案:2
27、(江西省鹰潭市2008届高三第一次模拟)如图,在平面斜坐标中
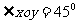 ,斜坐标定义为
,斜坐标定义为 (其中
(其中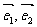 分别为
分别为
 斜坐标系的x轴,y轴的单位向量),则点P的坐标为
斜坐标系的x轴,y轴的单位向量),则点P的坐标为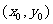 。若
。若
 且动点
且动点 满足
满足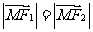 ,则点M在
,则点M在
斜坐标系中的轨迹方程为
答案:x+y=0
26、(江西省鹰潭市2008届高三第一次模拟)在锐角三角形△ABC中,已知| →AB|=4,| →AC|=1,△ABC的面积为,则→AB·→AC的值为___________
答案:2
25、(江苏省盐城市2008届高三六校联考)若向量 满足
满足 ,则向量
,则向量 的夹角大小为
的夹角大小为
答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com