5．已知平面向量a＝(1,2)，b＝(－2，m)，且a∥b，则2a+3b＝________.

解析：由a＝(1,2)，b＝(－2，m)，且a∥b，得1×m＝2×(－2)⇒m＝－4，从而a＝(1,2)，b＝(－2，－4)，那么2a+3b＝2(1,2)+3(－2，－4)＝(－4，－8)．

答案：(－4，－8)

2．(★★★★)如右图所示，设P、Q为△ABC内的两点，且＝+，＝+，则△ABP的面积与△ABQ的面积之比为________．

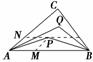
解析：如图所示，设＝，＝，则＝+，由向量的平行四边形法则，知NP∥AB，所以＝＝，

同理可得＝，故＝.

1．(2010·创新题)已知等差数列{a_n}的前n项和为S_n，若＝a₁+a_{2 010}，且A、B、C三点共线(该直线不过点O)，则S_{2 010}等于(　)

A．1 004　 　 　B．1 005 　　　 　C．2 010　 　　 　D．2 011

解析：∵A、B、C三点共线，

∴存在一个实数λ，使＝λ，即－＝λ(－)，∴＝(1－λ) +λ.

又∵＝a₁+a_{2 010}，∴a₁+a_{2 010}＝(1－λ)+λ＝1，

∴S_{2 010}＝×2 010＝1 005.

答案：C

10．如图所示，在△ABC中，D、F分别是BC、AC的中点，＝，＝a，＝b.

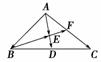
(1)用a、b表示向量、、、、；(2)求证：B、E、F三点共线．

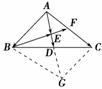
解答：(1)延长AD到G，使＝，

连接BG、CG，得到▱ABGC，所以＝a+b，

＝＝(a+b)，＝＝(a+b)．

＝＝b，＝－＝(a+b)－a＝(b－2a)．

＝－＝b－a＝(b－2a)．

(2)证明：由(1)可知＝，所以B、E、F三点共线．

9．(2010·安徽合肥调研)若a，b是两个不共线的非零向量，a与b起点相同，则当t为何值时，a，tb，(a+b)三向量的终点在同一条直线上？

解答：设OA＝a，＝tb，＝(a+b)，∴＝－＝－a+b，＝－＝tb－a.

要使A、B、C三点共线，只需＝λ.即－a+b＝λtb－λa.

∴有⇒∴当t＝时，三向量终点在同一直线上．

8．设两个非零向量a与b不共线，

(1)若＝a+b，＝2a+8b，＝3(a－b)，求证：A、B、D三点共线；

(2)试确定实数k，使ka+b和a+kb共线．

证明：(1)∵＝a+b，＝2a+8b，＝3(a－b)，

∴＝+＝2a+8b+3(a－b)＝2a+8b+3a－3b＝5(a+b)＝5.

∴、共线．又它们有公共点B，∴A、B、D三点共线．

(2)解答：∵ka+b与a+kb共线，∴存在实数λ，使ka+b＝λ(a+kb)，

即ka+b＝λa+λkb，∴(k－λ)a＝(λk－1)b.

∵a、b是不共线的两个非零向量，∴k－λ＝λk－1＝0，∴k²－1＝0.∴k＝±1.

7．在△ABC中，＝a，＝b，M是CB的中点，　　 N是AB的中点，且CN、AM交于点P，则可用a、b表示为________．

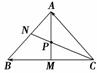
解析：如图所示，＝+＝－+

＝－+×(+)＝－++

＝－+＝－a+b.

答案：－a+b

6．(2010·浙江杭州调研)设a、b是两个不共线向量，＝2a+pb，＝a+b，＝a－2b，若A、B、D三点共线，则实数p的值是________．

解析：∵＝+＝2a－b，又A、B、D三点共线，∴存在实数λ，使＝λ.

即，∴p＝－1.

答案：－1

5．(2009·宁夏银川模拟)若＝3e₁，＝－5e₁，且与的模相等，则四边形ABCD是________．

解析：∵＝－，∴AB∥CD，且|AB|≠|CD|.

答案：等腰梯形

4．已知平面内有一点P及一个△ABC，若++＝，则(　)

A．点P在△ABC外部　 B．点P在线段AB上

C．点P在线段BC上　 D．点P在线段AC上

解析：∵++＝，∴++＝－

∴＝－2.∴2＝，∴点P在线段AC上．

答案：D