4．sin 163°sin 223°+sin 253°sin 313°等于(　)

A．－　 　　　　　 B.　 　C．－　 　D.

解析：原式＝sin 163°·sin 223°+cos 163°cos 223°＝cos(163°－223°)＝cos(－60°)＝.

答案：B

3．等式|sin αcos α|+|sin²α－cos²α|＝成立的充要条件是(　)

A．α＝kπ(k∈Z)　 　　　　　　　　 B．α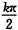＝(k∈Z)

C．α＝(k∈Z)　 　　　　　　　　 D．α＝(k∈Z)

解析：由题意知：原式＝|sin 2α|+|cos 2α|＝

∴|sin 2α|+|cos 2α|＝1，∴1+2|sin 2αcos 2α|＝1，|sin 4α|＝0，α＝(k∈Z)．

答案：C

2．下列各式中，值为的是(　)

A．2sin 15°cos 15°　 　　　 B．cos²15°－sin²15°

C．2sin²15°－1　 　　　　　　 D．sin²15°+cos²15°

解析：cos²15°－sin²15°＝cos 30°.

答案：B

1．若tan α＝3，tan β＝，则tan(α－β)等于(　)

A．－3　 　　　　　 　B．－　 　　　　 C．3　 　　　 D.

解析：tan(α－β)＝＝＝＝.

答案：D

5．coscosπ的值是________．

解析：原式＝·2sincoscos＝·2sincosπ＝sinπ＝.

4．已知x∈(－，0)，cos x＝，则tan 2x等于(　)

A.　 　　　　B．－　 　　　　C.　 　　　　　D．－

解析：x∈(－，0)，cos x＝，∴sin x＝－，tan x＝＝－.

∴tan 2x＝＝－.

答案：D

3．tan－cot等于(　)

A．4　 　　　　B．－4 　　　　　C．2　 　　　　　D．－2

解析：原式＝－＝＝＝－2.

答案：D

2．已知sin α+sin β+sin γ＝0，cos α+cos β+cos γ＝0，则cos(α－β)的值为(　)

A．1　 　　　B．－1 　　　　C.　 　　　　　D．－

解析：将已知两式化为sin α+sin β＝－sin γ，cos α+cos β＝－cos γ.两式平方相加，有cos(α－β)＝－.

答案：D

1．在△ABC中，已知2sin A cos B＝sin C，那么△ABC一定是(　)

A．直角三角形　 　　B．等腰三角形　 　　C．等腰直角三角形　 　　D．正三角形

答案：B

5．(2009·北京东城一模)已知两个向量a＝(1,2)，b＝(x,1)，若(a+2b)∥(2a－2b)，则x的值为________．

解析：a+2b＝(1+2x,4),2a－2b＝(2－2x,2)，

∵(a+2b)∥(2a－2b)，∴(1+2x)×2－(2－2x)×4＝0，∴x＝.