
2.距离船只A的正北方向100海里处有一船只B,以每小时20海里的速度,沿北偏西60°角的方向行驶,A船只以每小时15海里的速度向正北方向行驶,两船同时出发,问几小时后两船相 距最近?
解:设t小时后A行驶到点C,B行驶到点D,则BD=20 BC=100-15t
过D作DE^BC于E DE=BDsin60°=10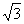 t BE=BDcos60°=10t
t BE=BDcos60°=10t
∴EC=BC+BE=100-5t
CD=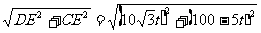 =
=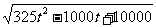
∴t=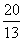 时CD最小,最小值为200
时CD最小,最小值为200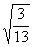 ,即两船行驶
,即两船行驶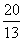 小时相距最近
小时相距最近
1.如图,已知⊙O的半径为R,由直径AB的端点B作圆的切线,从圆周上任一点P引该切线的垂线,垂足为M,连AP设AP=x
⑴写出AP+2PM关于x的函数关系式 ⑵求此函数的最值
解:⑴过P作PD^AB于D,连PB
设AD=a则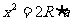
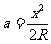
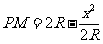
∴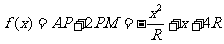
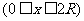
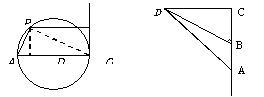 ⑵
⑵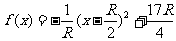
当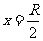 时
时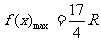
当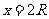 时
时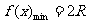
例1(课本第86页 例2)设海拔 x m处的大气压强是 y Pa,y与
x 之间的函数关系式是 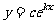 ,其中
c,k为常量,已知某地某天在海平面的大气压为
,其中
c,k为常量,已知某地某天在海平面的大气压为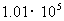 Pa,1000 m高空的大气压为
Pa,1000 m高空的大气压为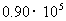 Pa,求:600 m高空的大气压强(结果保留3个有效数字)
Pa,求:600 m高空的大气压强(结果保留3个有效数字)
解:将 x = 0 , y =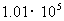 ;x = 1000 , y =
;x = 1000 , y =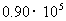 ,
代入
,
代入 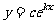 得:
得:

将 (1) 代入 (2) 得:
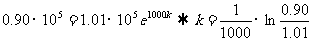
计算得: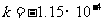 ∴
∴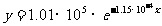
将 x = 600 代入, 得: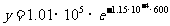
计算得: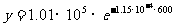 =0.943×105(Pa)
=0.943×105(Pa)
答:在600 m高空的大气压约为0.943×105Pa.
说明:(1)此题利用数学模型解决物理问题;(2)需由已知条件先确定函数式;(3)此题实质为已知自变量的值,求对应的函数值的数学问题;(4)此题要求学生能借助计算器进行比较复杂的运算.
例2在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到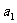 ,
,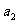 ,……,
,……, 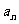 共n个数据,我们规定所测量的物理量的“最佳近似值”a是这样一个量:与其他近似值比较a与各数据差的平方和最小.依次规定,从
共n个数据,我们规定所测量的物理量的“最佳近似值”a是这样一个量:与其他近似值比较a与各数据差的平方和最小.依次规定,从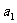 ,
,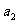 ,……,
,……, 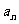 推出的a=________.(1994年全国高考试题)
推出的a=________.(1994年全国高考试题)
分析:此题应排除物理因素的干扰,抓准题中的数量关系,将问题转化为函数求最值问题.
解:由题意可知,所求a应使y=(a-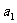 )
)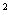 +(a-
+(a-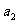 )
)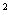 +…+(a-
+…+(a-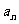 )
)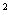 最小
最小
由于y=na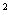 -2(
-2(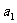 +
+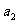 +…+
+…+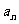 )a+(
)a+(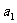
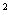 +
+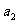
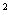 +…+
+…+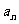
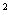 )
)
若把a看作自变量,则y是关于a的二次函数,于是问题转化为求二次函数的最小值.
因为n>0,二次函数f(a)图象开口方向向上.
当a=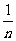 (
(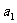 +
+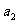 +…+
+…+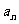 ),y有最小值.
),y有最小值.
所以a=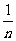 (
(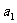 +
+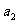 +…+
+…+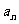 )即为所求.
)即为所求.
说明:此题在高考中是具有导向意义的试题,它以物理知识和简单数学知识为基础,并以物理学科中的统计问题为背景,给出一个新的定义,要求学生读懂题目,抽象其中的数量关系,将文字语言转化为符号语言,即
y=(a-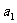 )
)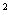 +(a-
+(a-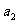 )
)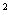 +…+(a-
+…+(a-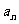 )
)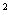 ,然后运用函数的思想、方法去解决问题,解题关键是将函数式化成以a为自变量的二次函数形式,这是函数思想在解决实际问题中的应用.
,然后运用函数的思想、方法去解决问题,解题关键是将函数式化成以a为自变量的二次函数形式,这是函数思想在解决实际问题中的应用.
例3某种放射性元素的原子数N随时间t的变化规律是N=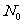
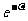 ,其中
,其中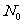 ,λ是正的常数.
,λ是正的常数.
(1)说明函数是增函数还是减函数;(2)把t表示成原子数N的函数;(3)求当N=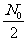 ?时,t的值.
?时,t的值.
解:(1)由于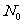 >0,λ>0,函数N=
>0,λ>0,函数N=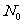
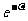 是属于指数函数y=
是属于指数函数y=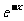 类型的,所以它是减函数,即原子数N的值随时间t的增大而减少
类型的,所以它是减函数,即原子数N的值随时间t的增大而减少
(2)将N=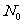
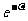 写成
写成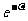 =
=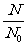
根据对数的定义有-λt=ln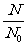
所以t=-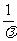 (lnN-ln
(lnN-ln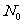 )=
)=
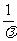 (ln
(ln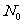 -lnN)
-lnN)
(3)把N=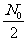 代入t=
代入t=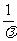 (ln
(ln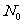 -lnN)得t=
-lnN)得t=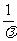 (ln
(ln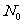 -ln
-ln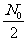 )
)
=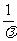 (ln
(ln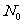 -ln
-ln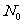 +ln2)=
+ln2)=
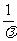 ln2.
ln2.
上一节课,我们主要学习了有关增长率的数学模型,这种模型在有关产量、产值、粮食、人口等等增长问题常被用到.这一节,我们学习有关物理问题的数学模型
5.在△ABC中,sin A+cos A=,则=________.
解析:由已知2sin Acos A=-,∴cos A<0,即A为钝角,∴(sin A-cos A)2=,
∴sin A-cos A=,则sin A=,cos A=-.原式=.
4.若钝角三角形三内角成等差数列,且最大边长与最小边长的比值为m,则m的范围是( )
A.(1,2) B.(2,+∞) C.[3,+∞) D.(3,+∞)
解析:设△ABC三内角为A、B、C,其对边为a、b、c,且A<B<C,由2∠B=∠A+∠C,且∠A+∠B+∠C=180°,可得∠B=60°,由已知∠A<30°.m====cot A+>2.
答案:B
3.在△ABC中,设命题p:==,命题q:△ABC是等边三角形,那么命题p是命题q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:若△ABC是等边三角形,则==;若==,
又==,则即a=b=c.∴p是q的充要条件.
答案:C
2.在△ABC中,已知∠B=45°,c=2,b=,则∠A等于( )
A.15° B.75° C.105° D.75°或15°
解析:根据正弦定理= ,sin C===.
∴C=60°或C=120°,因此A=75°或A=15°.
答案:D
1.在△ABC中,若∠A=60°,b=1,S△ABC=,则的值为( )
A. B. C. D.
解析:∵S△ABC=,即bcsin A=,∴c=4.由余弦定理a2=b2+c2-2bccos A=13,∴a=,
∴===.
答案:B
5.若cos(α+β)=,cos(α-β)=,则tan α·tan β=________.
解析:∵cos(α+β)=cos αcos β-sin αsin β=①
cos(α-β)=cos αcos β+sin αsin β=②
由①②解得cos αcos β=,sin αsin β=,则tan αtan β==.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com