
6. 设{an}的首项为1的正项数列,且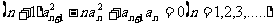 则它的通项公式为an=
。
则它的通项公式为an=
。
简答.提示:1.A;2.C; 由-n2+10n+11≥0得-1≤n≤11,又n∈N*,∴0<n≤11.∴前10项为正,第11项为0; 3.2n+1-3; 4. an = 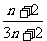 ; 5. an=1+
; 5. an=1+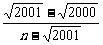 ,又44<
,又44<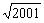 <45,
<45,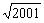 -
-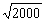 >0,故第45项最大,第44项最小; 6.由由已知a1=1 ,
>0,故第45项最大,第44项最小; 6.由由已知a1=1 , 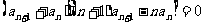
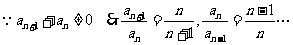 连乘得
连乘得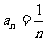
[解答题]
5.已知an=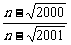 ,且数列{an}共有100项,则此数列中最大项为第________项,最小项为第__________项.
,且数列{an}共有100项,则此数列中最大项为第________项,最小项为第__________项.
4. 数列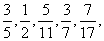 ……的通项公式是
……的通项公式是
3.(2006重庆)在数列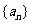 中,若
中,若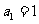 ,
,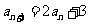
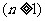 ,则该数列的通项
,则该数列的通项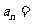 。
。
2.设an=-n2+10n+11,则数列{an}从首项到第几项的和最大 ( ).
A.10 B.11 C.10或11 D.12
[填空题]
1.已知数列{an}中,a1=1,a2=3,an=an-1+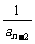 (n≥3),则a5等于 ( )
(n≥3),则a5等于 ( )
A.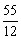 B.
B.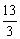 C.4 D.5
C.4 D.5
3.题型.思想.方法:求数列的通项公式的主要方法有
(1)由数列的前几项归纳出一个通项公式,关键是善于观察.
(2)利用an 与Sn的关系,不要忘记验证a1 能否与n≥2时an的式子统一;
(3) 由递推公式求通项公式,常化归为等差等比数列,或用利用迭加an-an-1=f(n)、迭乘an/an-1=f(n)、迭代等方法.
同步练习 3.2 数列 通项公式
[选择题]
2.an与Sn的关系是十分重要的考点;
1.数列、通项公式、递推公式、前n项和等概念;
3.求和Tn时,化为”一正一负连续两项,累加相消.
[研讨.欣赏](2006全国Ⅱ)数列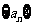 的前n项和为
的前n项和为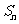 ,且方程
,且方程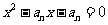 有一根为
有一根为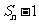 ,n=1,2,3…. (I)求
,n=1,2,3…. (I)求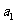 ,
,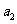 ; (II)求
; (II)求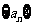 的通项公式;
的通项公式;
解:(Ⅰ)当n=1时,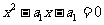 有一根为
有一根为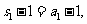
于是 解得
解得 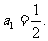
当n=2时,有一根为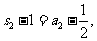
于是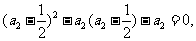 解得
解得 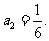
(Ⅱ)由题设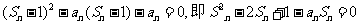
当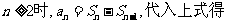
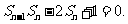 ①
①
由(Ⅰ)知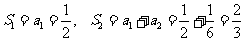
由1可得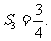 由此猜想
由此猜想 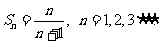
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即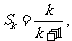
当n=k+1时,由1得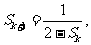 即
即 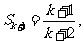
故n=k+1时结论也成立,
综上,由(i)、(ii)可知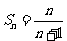 对所有正数n都成立,
对所有正数n都成立,
于是当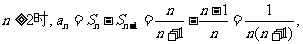 又n=1时,
又n=1时,
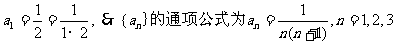
方法提炼:先用数学归纳法求Sn再求通项公式an.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com