
2.由an=4an-1+2n两边同除以2n得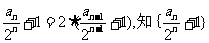 是等比数列.
是等比数列.
2.法二:也可以由Sn与an的关系,先转化为Sn与Sn-1的关系,求出Sn再求an.此法虽绕些,但也是一种方法.
[例3]已知数列{an}的通项an = (n+1)(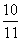 )n (n∈N﹡)试问该数列有没有最大项?若有,求出最大项和最大项的项数;若没有,说明理由
)n (n∈N﹡)试问该数列有没有最大项?若有,求出最大项和最大项的项数;若没有,说明理由
解:∵an + 1
– an = (n+2)( 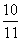 )n+1 – (n+1) (
)n+1 – (n+1) ( 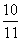 )n =
)n = 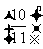

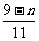
∴当n<9时,a n + 1 - an>0即a n + 1 >a n ;
当n=9时a n + 1-a n=0,即a n + 1=an ,
当n>9时,a n + 1- an<0即a n + 1<a n ,
故a1<a2<……<a9 = a10>a11>a12>……,
∴数列{an}中最大项为a9或a10 ,
其值为10·(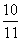 )9,其项数为9或10
)9,其项数为9或10 
法二:由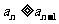 解得n≤10,又
解得n≤10,又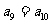 .所以最大项为a9或a10.
.所以最大项为a9或a10.
方法提炼:由an + 1 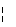 an 判断增减情况,再确定最大项;注意等号.
an 判断增减情况,再确定最大项;注意等号.
法二:由通项公式,利用导数求最大项也行.
[例4] (2006全国Ⅰ)设数列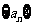 的前
的前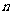 项的和
项的和
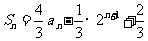 ,
,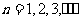
(Ⅰ)求首项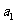 与通项
与通项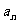 ;
;
(Ⅱ)设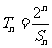 ,
,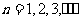 ,证明:
,证明: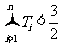
解: (Ⅰ)由 Sn=an-×2n+1+, n=1,2,3,… ①
得 a1=S1= a1-×4+ 所以a1=2
再由①有 Sn-1=an-1-×2n+, n=2,3,4,……②
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n),n=2,3, …
整理得: an+2n=4(an-1+2n-1),n=2,3, … , 因而数列{ an+2n}是首项为a1+2=4,公比为4的等比数列,即 : an+2n=4×4n-1= 4n, n=1,2,3, …, 因而an=4n-2n, n=1,2,3, …,
(Ⅱ)将an=4n-2n代入①得 Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×( - )
所以, 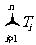 =
= 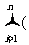 - ) = ×( -
- ) = ×( - 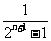 ) <
) <
提炼方法;1. 利用an=Sn-Sn-1和已知得:an=4an-1+2n,令:an+x22=4(an-1+x2n-1)可得an+22=4(an-1+2n-1)化为等比数列;
[例1]有一数列{an},a1=a,由递推公式an+1=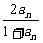 ,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
解:∵a1=a,an+1=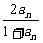 ,∴a2=
,∴a2=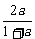 ,
,
a3=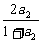 =
=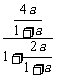 =
=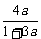 ,
,
a4=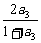 =
=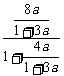 =
=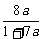 .
.
观察规律:an=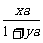 形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
∴an=
形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
∴an=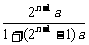 .下面再用数学紧地证明:
.下面再用数学紧地证明:
法二:由an+1=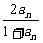 得
得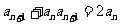 同除以
同除以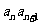 得
得
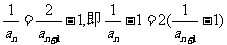 ,
,
∴当a=1时,an≡1;
当a≠1时,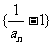 是等比数列.公比是
是等比数列.公比是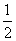 ,首项
,首项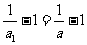
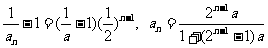 .当a=1时也适合此式.
.当a=1时也适合此式.
提炼方法:1.”猜想+证明”,即通过分析特殊的事例,归纳、猜想出一般规律,再用数学归纳法证明,这种探索问题的方法,在解数列问题时经常用到,应引起足够的重视.
2.由递推公式,化归为等比或等差数列再求.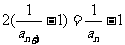 方法更为便捷.
方法更为便捷.
[例2] 已知数列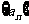 的前
的前 项和
项和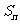 满足
满足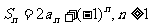

(1)写出数列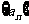 的前三项
的前三项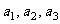 ;
;
(2)求数列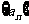 的通项公式;
的通项公式;
解:(1)为了计算前三项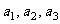 的值,只要在递推式
的值,只要在递推式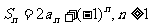 中,对
中,对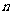 取特殊值
取特殊值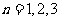 ,就可以消除解题目标与题设条件之间的差异
,就可以消除解题目标与题设条件之间的差异
由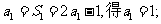
由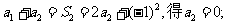
由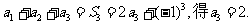
(2)为了求出通项公式,应先消除条件式中的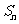
 事实上
事实上
当 时,由
时,由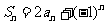 得
得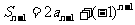
两式相减得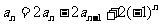 即
即 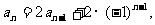
两边同乘以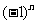 ,便得
,便得

令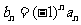 就有
就有 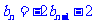 ,
,
于是 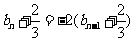 ,
,
这说明数列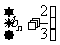 是等比数列,公比
是等比数列,公比 首项
首项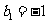 ,
,
从而,得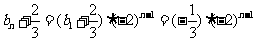 ,
,
即 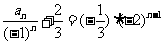 , 故有
, 故有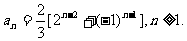
经验证a1也满足上式,故知 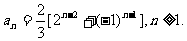
法二:迭代法: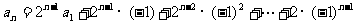
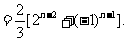
提炼方法:1.利用Sn与an的关系转化为an,an-1的递推关系: 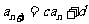 形式;再转化为等比数列.
形式;再转化为等比数列.
5. an
= 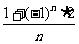 ; 6.由已知Sn=2n+1-1,故an=
; 6.由已知Sn=2n+1-1,故an=
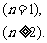
6.已知数列{an}的前n项和Sn满足log2(Sn+1)=n+1,求数列{an}的通项公式.
简答:1-3、ACC;1. 法一: a3=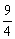 ,…a5=
,…a5=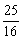 ,.法二:当n≥2时,a1·a2·…·an=n2.当n≥3时a1·a2·…·an-1=(n-1)2.两式相除an=(
,.法二:当n≥2时,a1·a2·…·an=n2.当n≥3时a1·a2·…·an-1=(n-1)2.两式相除an=(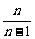 )2,…;2. 法一: an=
)2,…;2. 法一: an=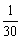 (-n2+15n-9),再解
(-n2+15n-9),再解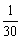 (-n2+15n-9)>1.5,得6<n<9.法二:将选项中的月份代入计算验证.4. f(3) =10,
(-n2+15n-9)>1.5,得6<n<9.法二:将选项中的月份代入计算验证.4. f(3) =10,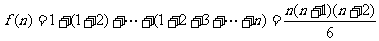
5.-1,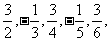 ……的通项公式是
……的通项公式是
4.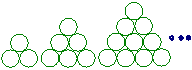 (2006广东) 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2
(2006广东) 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2 3
3 4
4 …堆最底层(第一层)分别按图4所示方式固定摆放
…堆最底层(第一层)分别按图4所示方式固定摆放 从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=
;f(n)= (答案用n表示)
从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=
;f(n)= (答案用n表示) 
3.2003年12月,全世界爆发"禽流感",科学家经过深入的研究,终于发现了一种细菌M在杀死"禽流感"病毒N的同时能够自身复制.已知1个细菌M可以杀死1个病毒N,并且生成2个细菌M,那么1个细菌M和2048个"禽流感"病毒N最多可生成细菌M的数值是 ( )
A 1024 B 2048 C 2049 D 22048
2.根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn=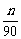 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是
( )
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是
( )
A.5、6月 B.6、7月 C.7、8月 D.8、9月
1.数列{an}中,a1=1,对于所有的n≥2,n∈N都有a1·a2·a3·…·an=n2,则a3+a5等于 ( )
A.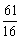 B.
B.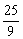 C.
C.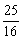 D.
D.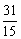
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com