
4.在成长的过程中,人们会有许多刻骨铭心的感动,也有许多让人回味、让人珍惜的感受和经历。
请以“回味”为题,写一篇不少于800字的文章,除诗歌外,文体不限。
3.以“凝聚”为题,写一篇文章。
要求:① 除诗歌外,文体不限。② 不少于800字。
2.以“脊梁”为题,写一篇文章。
要求:① 除诗歌外,文体不限。② 不少于800字。
1. 请以“分忧”为题,写一篇文章。
10.(2005江西)已知数列{an}的各项都是正数,且满足
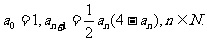
(1)证明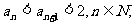
(2)求数列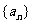 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=0时,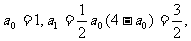 ∴
∴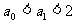 ,命题正确.
,命题正确.
2°假设n=k时有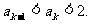 则
则
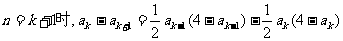
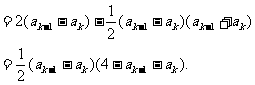
而
又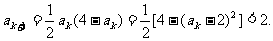 ∴
∴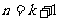 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有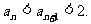
方法二:用数学归纳法证明:
1°当n=1时,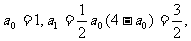 ∴
∴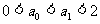 ;
;
2°假设n=k时有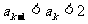 成立,令
成立,令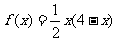 ,
,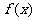 在[0,2]上单调递增,所以由假设有:
在[0,2]上单调递增,所以由假设有:
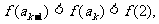 即
即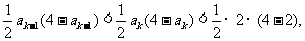
也即当n=k+1时 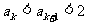 成立,所以对一切
成立,所以对一切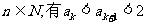
(2)下面来求数列的通项: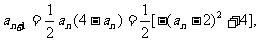 所以
所以
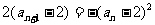
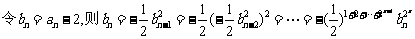 又bn=-1,
又bn=-1,
所以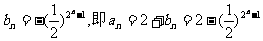
[探索题](2003全国)设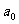 为常数,且
为常数,且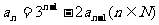
证明对任意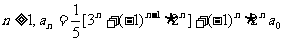 ;
;
证法一:(i)当n=1时,由已知a1=1-2a0,等式成立;
(ii)假设当n=k(k≥1)等式成立,则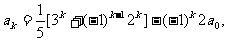
那么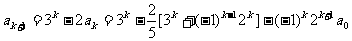
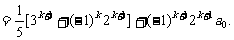
也就是说,当n=k+1时,等式也成立. 根据(i)和(ii),可知等式对任何n∈N,成立.
证法二:如果设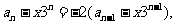 代
代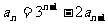 可得
可得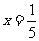 .
.
所以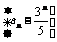 是公比为-2,首项为
是公比为-2,首项为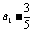 的等比数列.
的等比数列.
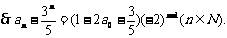 即
即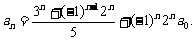
证法三: 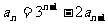 同除以3n得
同除以3n得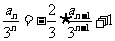 ,待定系数可解.
,待定系数可解.
9. 已知数列{an}中,an∈(0,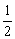 ),当n≥2时,an=
),当n≥2时,an=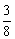 +
+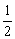 ·an-12,求证:数列{an}递增.
·an-12,求证:数列{an}递增.
证明:an+1-an=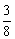 +
+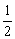 an2-an=
an2-an=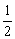 (an-1)2-
(an-1)2-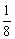 .
.
∵0<an<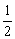 ,∴-1<an-1<-
,∴-1<an-1<-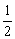 .
.
∴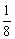 <
<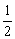 (an-1)2<
(an-1)2<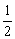 .
.
∴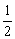 (an-1)2-
(an-1)2-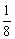 >0.
>0.
∴an+1-an>0,即an<an+1对一切自然数n都成立, 数列{an}递增.
8. 已知在正项数列{an}中,Sn表示前n项和且2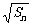 =an+1,求an
=an+1,求an
解:由已知2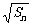 =an+1,得当n=1时,a1=1;当n≥2时,an=Sn-Sn-1,代入已知有2
=an+1,得当n=1时,a1=1;当n≥2时,an=Sn-Sn-1,代入已知有2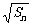 =Sn-Sn-1+1,即Sn-1=(
=Sn-Sn-1+1,即Sn-1=(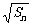 -1)2.又an>0,故
-1)2.又an>0,故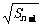 =
=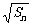 -1或
-1或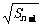 = 1-
= 1-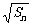 (舍),即
(舍),即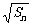 -
-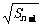 =1(n≥2),由定义得{
=1(n≥2),由定义得{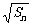 }是以1为首项,1为公差的等差数列,∴
}是以1为首项,1为公差的等差数列,∴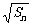 =n.故an=2n-1.
=n.故an=2n-1.
7.在数列{an}中,a1=1,an+1= ,求an.
,求an.
剖析:将递推关系式变形,观察其规律.
解:原式可化为 -
-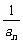 =n,
=n,
∴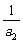 -
-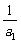 =1,
=1,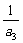 -
-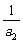 =2,
=2,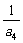 -
-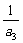 =3,…,
=3,…,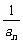 -
-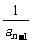 =n-1.
=n-1.
相加得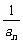 -
-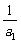 =1+2+…+(n-1),
∴an=
=1+2+…+(n-1),
∴an=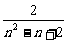 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com