
21.(本小题满分12分)
(理)已知数列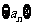 ,且
,且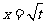 是函数
是函数 ,(
,(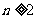 )的一个极值点.数列
)的一个极值点.数列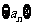 中
中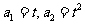 (
(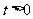 且
且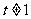 ).
).
(1)求数列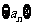 的通项公式;
的通项公式;
(2)记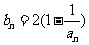 ,当
,当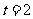 时,数列
时,数列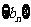 的前
的前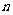 项和为
项和为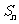 ,求使
,求使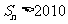 的
的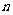 的最小值;
的最小值;
(3)若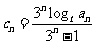 ,证明:
,证明: (
(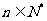 )。
)。
(文)已知函数f(x)=()x,x∈[-1,1],函数g(x)=f2(x)-2af(x)+3的最小值为h(a).
(1)求h(a)的解析式;
(2)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.
1----10;ACACC AABCD 11;29 12;4 13;-1/5 14;-2 15;(理)2,4(文)a>1或a=0或a<-1
16;
解: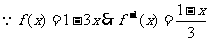
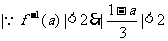
解,得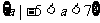
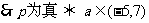 x
x
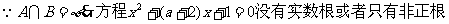
即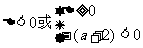 解得
解得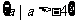
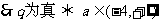
p和q中有且只有一个真命题,即p真q假或p假q真.
即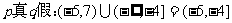

 [
[
17;
 解(1)n=1时,
解(1)n=1时,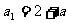
 时,
时,
∵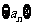 为等比数列 ∴
为等比数列 ∴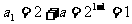 ∴
∴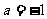
∴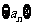 的通项公式为
的通项公式为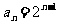 (6分)
(6分)
(2)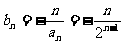
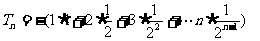 ①[
①[ 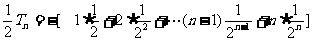 ②
②
②-①得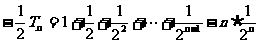
∴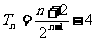
18; 解:(1)y=.
(2)当100≤x≤200时,w=xy-40y-(480+1520)
将y=-x+28代入上式得:
w=x(-x+28)-40(-x+28)-2000=-(x-195)2-78,
当200<x≤300时,同理可得:w=-(x-180)2-40,
故w=.
若100≤x≤200,当x=195时,wmax=-78,
若200<x≤300,wmax=-80.
19;解:(理)(1)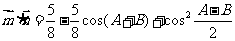
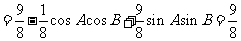
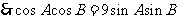 ,
, ……………………5分
……………………5分
(2)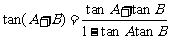
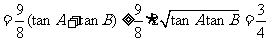 …………8分
…………8分
(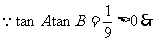 A,B均是锐角,即其正切均为正)
A,B均是锐角,即其正切均为正)
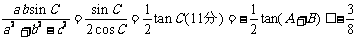
所求最大值为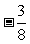 。…………………………………………12分
。…………………………………………12分
20;解:(Ⅰ)由已知 ,
, 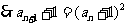
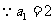
 ,两边取对数得
,两边取对数得
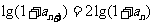 ,即
,即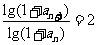
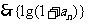 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅱ)当 时,
时,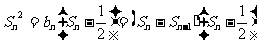 展开整理得:
展开整理得: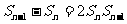 ,若
,若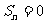 ,则有
,则有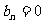 ,则
,则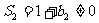 矛盾,所以
矛盾,所以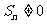 ,所以在等式两侧同除以
,所以在等式两侧同除以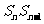 得
得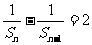 ,
,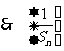 为等差数列
为等差数列
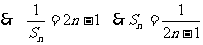
(Ⅲ)由(Ⅰ)知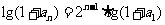
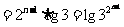
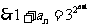
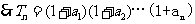
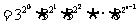
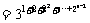 =
=
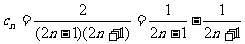
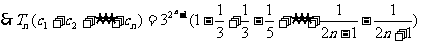
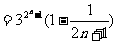
21;解:(理)(1) ,
,
所以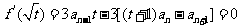 ,整理得
,整理得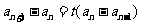
当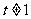 时,
时, 是以
是以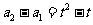 为首项,
为首项,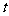 为公比的等比数列,
为公比的等比数列,
所以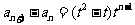
方法一:由上式得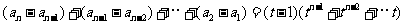
所以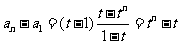 ,所以
,所以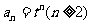 。
。
当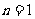 时上式仍然成立,故
时上式仍然成立,故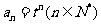 ……………4分
……………4分
方法二:由上式得: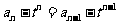 ,所以
,所以 是常数列
是常数列
,
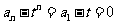 ,
,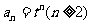 。
。
又,当 时上式仍然成立,故
时上式仍然成立,故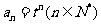
(2)当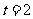 时,
时,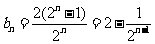

由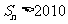 ,得
,得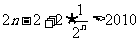 ,
,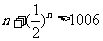 ,
,
当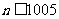 时,
时,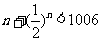 ,当
,当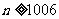 时,
时,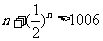
因此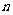 的最小值为1006.……………8分
的最小值为1006.……………8分
(3)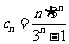 ,
,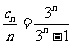 ,所以证明
,所以证明 ,
,
即证明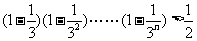
因为 ,
,
所以 ,从而原命题得证………12分
,从而原命题得证………12分

2)当a≥3时,h(a)=-6a+12,故m>n>3时,h(a)在[n,m]上为减函数,
所以h(a)在[n,m]上的值域为[h(m),h(n)].
由题意,则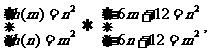 有,
有,
两式相减得6n-6m=n2-m2,
又m≠n,所以m+n=6,这与m>n>3矛盾,
故不存在满足题中条件的m,n的值.
20.(本小题满分12分)
已知数列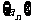 中
中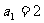 ,点
,点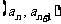 在函数
在函数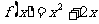 的图象上,
的图象上,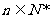 .数列
.数列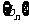 的前n项和为
的前n项和为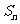 ,且满足
,且满足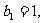 当
当 时,
时,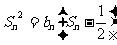
(1)证明数列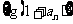 是等比数列;
是等比数列;
(2)求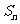 ;
;
(3)设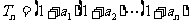 ,
,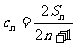 ,求
,求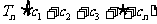 的值.
的值.
19.(本小题满分12分)
(理)已知角A、B、C是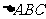 的三个内角,若向量
的三个内角,若向量 ,
,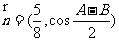 ,且
,且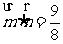 .
.
(1)求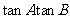 的值; (2)求
的值; (2)求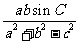 的最大值
的最大值
(文)设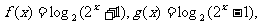 若关于
若关于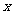 的函数
的函数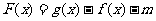 在
在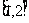 上有零点,求
上有零点,求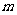 的取值范围。
的取值范围。
18. (本小题满分13分)
某公司用480万元购得某种产品的生产技术后,再次投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为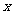 (元),年销售量为
(元),年销售量为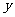 (万件),年获利为
(万件),年获利为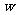 (万元).
(万元).
(1)请写出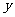 与
与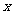 之间的函数关系式;
之间的函数关系式;
(2)求第一年的年获利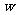 与
与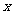 之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
17.(本小题满分13分)
设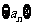 为等比数列,且其满足:
为等比数列,且其满足: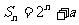 .
.
(1)求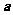 的值及数列
的值及数列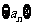 的通项公式;
的通项公式;
(2)已知数列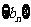 满足
满足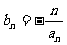 ,求数列
,求数列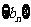 的前n项和
的前n项和 .
.
16.(本小题满分13分)
已知p: 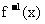 是
是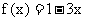 的反函数, 且
的反函数, 且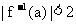 ;q : 集合
;q : 集合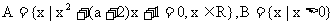 且
且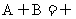 .求实数
.求实数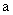 的取值范围, 使p或q为真,P且q为假。
的取值范围, 使p或q为真,P且q为假。
15.(理)数列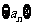 中,
中, 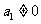 ,
,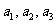 成等差数列;
成等差数列; 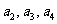 成等比数列;
成等比数列;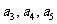 的倒数成等差数列.则①
的倒数成等差数列.则①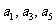 成等差数列;②
成等差数列;②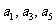 成等比数列; ③
成等比数列; ③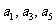 的倒数成等差数列; ④
的倒数成等差数列; ④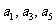 的倒数成等比数列.则其中正确的结论是 .
的倒数成等比数列.则其中正确的结论是 .
(文)函数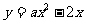 图像上有且仅有两个点到x轴的距离等于1,则a的取值范围是 .
图像上有且仅有两个点到x轴的距离等于1,则a的取值范围是 .
14.方程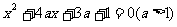 的两根为
的两根为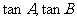 ,且
,且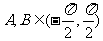 ,则
,则
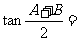 。
。
13.函数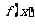 对于任意实数
对于任意实数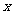 满足条件
满足条件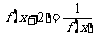 ,若
,若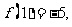 则
则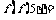 _______.
_______.
12.已知函数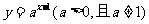 的图象恒过定点A,若点A在一次函数
的图象恒过定点A,若点A在一次函数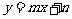 的图象上,其中
的图象上,其中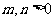 ,则
,则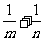 的最小值为
.
的最小值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com