
一分题(共8分)
1.下列人类的疾病中,不是由病毒引起的 ( )
A.腮腺炎 B.乙型肝炎 C.肺结构 D.脊髓灰质炎症
(二)填空题:
8、(07湖南)在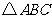 中,角
中,角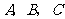 所对的边分别为
所对的边分别为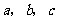 ,若
,若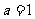 ,b=
,b=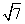 ,
,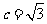 ,则
,则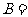 ;
;
9、(07北京)在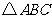 中,若
中,若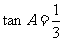 ,
,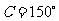 ,
,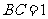 ,则
,则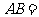 ;
;
10、(06全国Ⅱ)已知△ABC的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为 。
 (三)解答题:
(三)解答题:
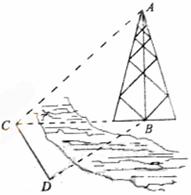
11、(07海南17)如图,测量河对岸的塔高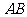 时,可以选与塔底
时,可以选与塔底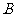 在同一水平面内的两个测点
在同一水平面内的两个测点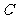 与
与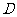 .现测得
.现测得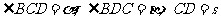 ,并在点
,并在点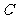 测得塔顶
测得塔顶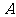 的仰角为
的仰角为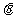 ,求塔高
,求塔高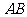 .
.
12、(07全国Ⅱ)在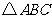 中,已知内角
中,已知内角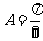 ,边
,边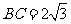 .设内角
.设内角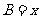 ,周长为
,周长为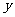 .
.
(1)求函数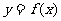 的解析式和定义域;
的解析式和定义域;
(2)求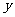 的最大值。
的最大值。
13、(07全国Ⅰ)设锐角三角形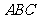 的内角
的内角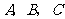 的对边分别为
的对边分别为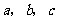 ,
,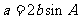 .
.
(Ⅰ)求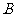 的大小;
的大小;
(Ⅱ)求 的取值范围。
的取值范围。
(一)选择题:
1、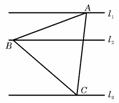 (07四川)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,
(07四川)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,
l2与l3间的距离是2,正三角形ABC的三顶点分别在l1、l2、l3上,
则△ABC的边长是( )
A、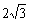 B、
B、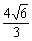 C、
C、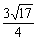 D、
D、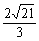
2、(07重庆)在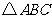 中,
中,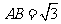 ,
,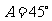 ,
,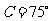 ,则
,则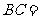 ( )
( )
A、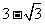 B、
B、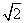 C、
C、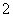 D、
D、
3、(06安徽11)如果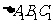 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于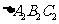 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A、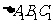 和
和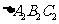 都是锐角三角形 B、
都是锐角三角形 B、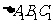 和
和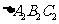 都是钝角三角形
都是钝角三角形
C、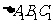 是钝角三角形,
是钝角三角形,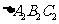 是锐角三角形
是锐角三角形
D、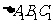 是锐角三角形,
是锐角三角形,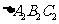 是钝角三角形
是钝角三角形
4、(06海南)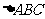 的内角
的内角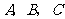 的对边分别为
的对边分别为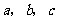 ,若
,若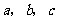 成等比数列,且
成等比数列,且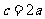 ,则
,则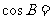 ( )
( )
A、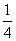 B、
B、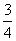 C、
C、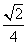 D、
D、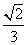
5、(05江苏)△ABC中,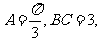 则△ABC的周长为( )
则△ABC的周长为( )
A、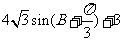 B、
B、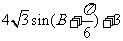
C、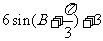 D、
D、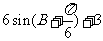
6、(04全国Ⅲ10)在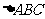 中,
中,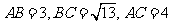 ,则边
,则边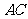 上的高为( )
上的高为( )
A、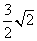 B、
B、 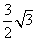 C、
C、 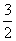 D、
D、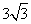
7、(04全国Ⅳ11)△ABC中,a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列,∠B=30°,△ABC的面积为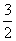 ,那么b=( )
,那么b=( )
A、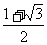 B、
B、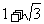 C、
C、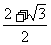 D、
D、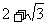
例1、(07广东16) 已知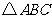 顶点的直角坐标分别为
顶点的直角坐标分别为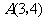 ,
,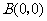 ,
,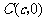 .
.
(1)若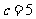 ,求
,求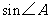 的值;
的值;
(2)若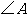 是钝角,求
是钝角,求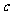 的取值范围.
的取值范围.
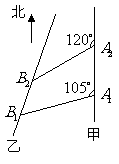 例2、(07山东20)如图,甲船以每小时
例2、(07山东20)如图,甲船以每小时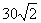 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于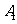 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西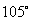 方向的
方向的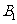 处,此时两船相距
处,此时两船相距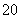 海里,当甲船航行
海里,当甲船航行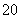 分钟到达
分钟到达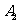 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西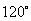 方向的
方向的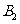 处,此时两船相距
处,此时两船相距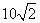 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
例3、(07福建17)在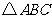 中,
中,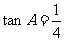 ,
,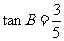 .
.
(Ⅰ)求角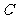 的大小;
的大小;
 (Ⅱ)若
(Ⅱ)若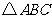 最大边的边长为
最大边的边长为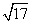 ,求最小边的边长.
,求最小边的边长.
例4、(06天津17)如图,在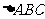 中,
中,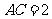 ,
,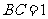 ,
,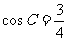 .
.
(1)求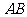 的值;(2)求
的值;(2)求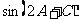 的值。
的值。
例5、(05全国Ⅲ19)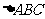 中,内角
中,内角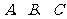 的对边分别是
的对边分别是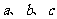 ,已知
,已知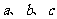 成等比数列,且
成等比数列,且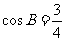 。(Ⅰ)求
。(Ⅰ)求 的值;(Ⅱ)设
的值;(Ⅱ)设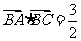 ,求
,求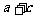 的值。
的值。
(三)解答题:
10、(07江西18)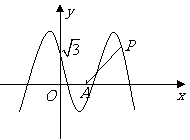 如图,函数
如图,函数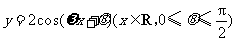 的图象与
的图象与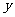 轴交于点
轴交于点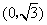 ,且在该点处切线的斜率为
,且在该点处切线的斜率为 .
.
(1)求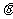 和
和 的值;
的值;
(2)已知点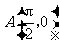 ,点
,点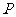 是该函数图象上一点,点
是该函数图象上一点,点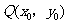 是
是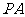 的中点,当
的中点,当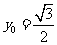 ,
, 时,求
时,求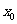 的值。
的值。
11、(07湖南16)已知函数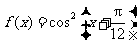 ,
,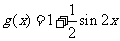 .
.
(I)设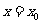 是函数
是函数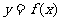 图象的一条对称轴,求
图象的一条对称轴,求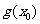 的值.
的值.
(II)求函数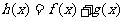 的单调递增区间。
的单调递增区间。
12、(06辽宁17)已知函数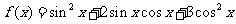 ,
,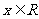 .求:
.求:
(I) 函数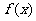 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量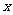 的集合;
的集合;
(II) 函数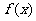 的单调增区间。
的单调增区间。
(二)填空题:
9、(07四川)下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是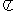 .
.
②终边在y轴上的角的集合是{a|a=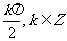 |.
|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数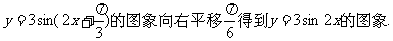
⑤函数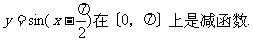
其中真命题的序号是 (写出所有真命题的序号)
(一)选择题:
1、(07福建)已知函数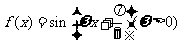 的最小正周期为
的最小正周期为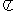 ,则该函数的图象( )
,则该函数的图象( )
A.关于点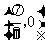 对称 B.关于直线
对称 B.关于直线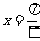 对称
对称
C.关于点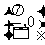 对称 D.关于直线
对称 D.关于直线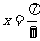 对称
对称
2、(07浙江)若函数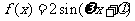 ,
,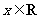 (其中
(其中 ,
,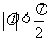 )的最小正周期是
)的最小正周期是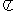 ,且
,且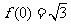 ,则( )
,则( )
A.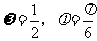 B.
B.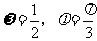
C.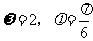 D.
D.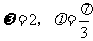
3、(06江苏)为了得到函数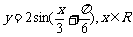 的图像,只需把函数
的图像,只需把函数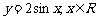 的图像上所有的点
的图像上所有的点
(A)向左平移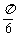 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的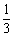 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移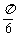 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的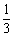 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移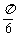 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移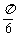 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
4、(06四川)下列函数中,图像的一部分如右图所示的是
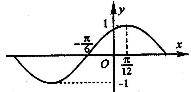 (A)
(A)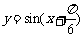 (B)
(B)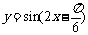
(C)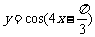 (D)
(D)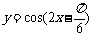
5、(06天津)已知函数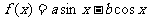 (
(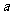

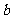 为常数,
为常数,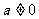 ,
,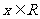 )在
)在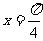 处取得最小值,则函数
处取得最小值,则函数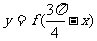 是( )
是( )
A.偶函数且它的图象关于点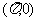 对称 B.偶函数且它的图象关于点
对称 B.偶函数且它的图象关于点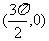 对称
对称
C.奇函数且它的图象关于点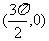 对称 D.奇函数且它的图象关于点
对称 D.奇函数且它的图象关于点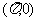 对称
对称
6、(06福建)已知函数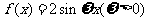 在区间
在区间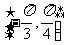 上的最小值是
上的最小值是 ,则
,则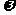 的最小值等于( )
的最小值等于( )
(A)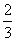 (B)
(B)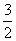 (C)2 (D)3
(C)2 (D)3
7、(05山东)函数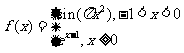 ,若
,若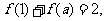 则
则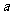 的所有可能值为
的所有可能值为
A、1
B、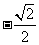 C、
C、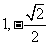 D、
D、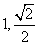
8、(05湖北)若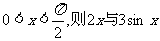 的大小关系( )
的大小关系( )
A、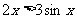 B、
B、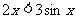 C、
C、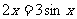 D、与x的取值有关
D、与x的取值有关
例1、(07安徽)函数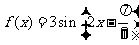 的图象为
的图象为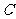 ,
,
①图象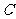 关于直线
关于直线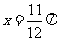 对称;
对称;
②函数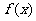 在区间
在区间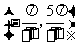 内是增函数;
内是增函数;
③由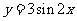 的图象向右平移
的图象向右平移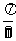 个单位长度可以得到图象
个单位长度可以得到图象 .
.
以上三个论断中,正确论断的个数是( )
A.0 B.1 C.2 D.3
例2、(07辽宁17)已知函数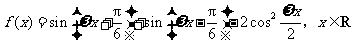 (其中
(其中 )。(I)求函数
)。(I)求函数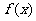 的值域;
的值域;
(II)若对任意的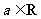 ,函数
,函数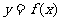 ,
,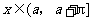 的图象与直线
的图象与直线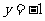 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定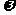 的值(不必证明),并求函数
的值(不必证明),并求函数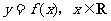 的单调增区间。
的单调增区间。
例3、(06山东17)已知函数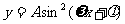 (A>0,
(A>0,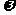 >0,0<
>0,0<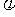 <
<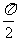 ),且
),且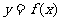 的最大值为2,其图象相邻两对称轴的距离为2,并过点(1,2)。
的最大值为2,其图象相邻两对称轴的距离为2,并过点(1,2)。
(1)求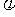 ;
;
(2)计算f(1)+f(2)+… +f(2 008)。
例4、(05湖南)设函数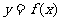 的图象与直线
的图象与直线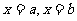 及x轴所围成图形的面积称为函数
及x轴所围成图形的面积称为函数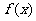 在
在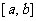 上的面积,已知函数
上的面积,已知函数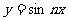 在[0,
在[0,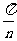 ]上的面积为
]上的面积为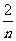 (
(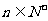 ),
),
(1)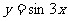 在[0,
在[0,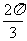 ]上的面积为 ;(2)
]上的面积为 ;(2)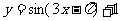 在[
在[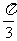 ,
,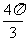 ]上的面积为 。
]上的面积为 。
(三)解答题:
11、(07四川17)已知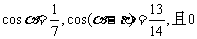 <
<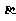 <
<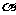 <
<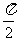 ,
,
(Ⅰ)求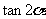 的值.
的值.
(Ⅱ)求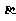 。
。
12、(05湖南)已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小。
(二)填空题:
7、(07上海)函数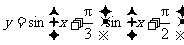 的最小正周期
的最小正周期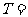 ;
;
8、(07江苏)若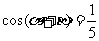 ,
,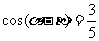 ,则
,则 _____;
_____;
9、(06上海春)在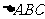 中,已知
中,已知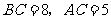 ,三角形的面积为12,则
,三角形的面积为12,则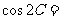 ;10、(06重庆)已知
;10、(06重庆)已知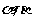
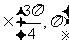 ,sin(
,sin( )=-
)=-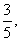 sin
sin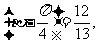
则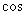
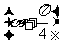 =________。
=________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com